Aperiodic Monotile - Ein-Stein, für aperiodische Muster
Isometric Grid of Einstein X (aperiodic monotile)
An aperiodic monotile, sometimes called an "einstein", is a shape that tiles the plane, but never periodically.
Einstein
P0, P1, ... P13 - P0 move point, P1 rotation point
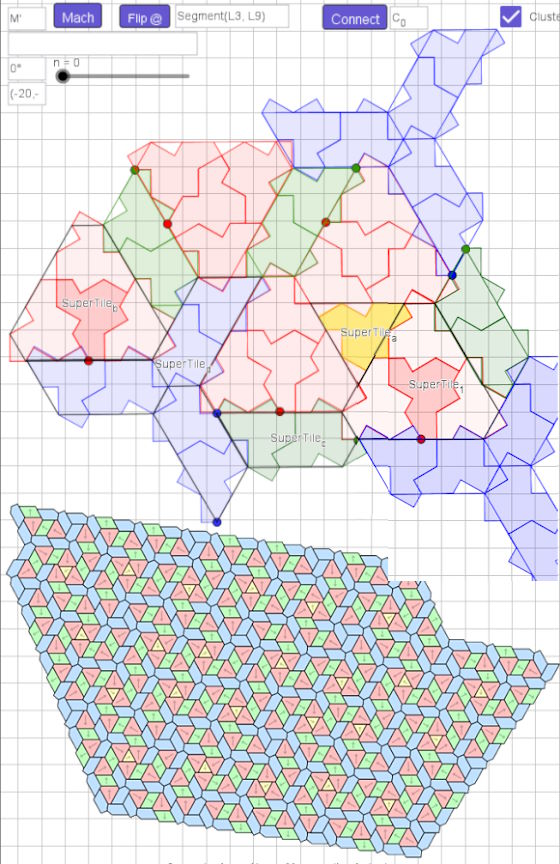
SuperTiles
SuperTileb = polyA', polyB', polyC' polyD'
Connect monotile to SuperTiles
A'0 connect B'0, (AB'0) , A'0 connect C'0, A'0 connect D'0
Grid: Isometric, n=13, L1...L13 Master Kachel
Li : Flip at Segment-Axis, M': Connect C_{0}, base M'_{0} - Move C_{0} by M'_{0}
Working with Isometric grid
I - Isometric Grid, X EinStein
I=Surface(O + u (cos(30°), sin(30°)) + v (cos(-30°), sin(-30°)), u, -10, 10, v, -10, 10)
X={O, I(1,-1), I(1,-1.5), I(2,-2), I(2.5,-3), I(2,-3), I(1.5,-2.5), I(1,-3), I(0,-2.5), I(0,-2), I(-1/2,-1.5), I(0,-1), I(-1/2, 0)}
J - Isometric Grid rotate α
α=0..360°
ROT={{cos(α), sin(α)}, {-sin(α), cos(α)}}
J=Surface((ROT (O + u (cos(30°), sin(30°)) + v (cos(-30°), sin(-30°)) - O)) + O, u, -10, 10, v, -10, 10)
Y={O, J(1,-1), J(1,-1.5), J(2,-2), J(2.5,-3), J(2,-3), J(1.5,-2.5), J(1,-3), J(0,-2.5), J(0,-2), J(-1/2,-1.5), J(0,-1), J(-1/2, 0)}
Isometric Grid XFig - Ein-Stein
XFig= {(0, 0), (1,-1), (1,-1.5), (2,-2), (2.5,-3), (2,-3), (1.5,-2.5), (1,-3), (0,-2.5), (0,-2), (-0.5,-1.5), (0,-1), (-0.5, 0)}
A anchor point: Fig_A=Polygon(A + Zip(I(pp), pp, XFig))
B anchor point: Fig_B=Polygon(B + Rotate(Zip(I(pp), pp, XFig), 30°))
Gruppierung von Kacheln in Clustern
Zusätzlich zu Vier-Kachel-Clustern, die aus einem Dreieck EinStein und seiner Drei-EinStein-Hülle, ein Sechseck, bestehen, identifizieren wir parallelogrammförmige Cluster, die aus Kachelpaaren bestehen.
Die Parallelogramme gibt es in zwei Varianten:
Die eine trennt zwei benachbarte Cluster und die andere verbindet sich mit zwei gedrehten Kopien zu einer dreiarmigen Propellerform, die Fylfot genannt wird.
A grouping of tiles into clusters in the example patch. In addition to four-tile clusters consisting of a reflected hat and its three-hat shell, we identify clusters consisting of a single tile, and parallelogram-shaped clusters consisting of pairs of tiles. The parallelograms come in two varieties: one separates two nearby shells, and the other joins up with two rotated copies to make a three-armed propeller shape called a fylfot.
Die Kachel zur Unendlichkeit
Rätsel Einstein-Kachel gelöst
An aperiodic monotile_{David Smith}
Two algorithms for randomly generating aperiodic tilings
Combinations of Metatiles (Struktur-Cluster)