M7-1. ZEREGINA: errealitatea argitzen
Errealitatearen edozein elementu aukeratu eta GeoGebraren bidez aztertu. Horretarako elementu horren irudia txertatu eta azterketari ekin (funtzioak, angeluak, proportzioak, etab). Ondoren, dokumentu batean azaldu nola jarriko zenuketen abian zuen ikasleekin jarduera hori.
https://en.m.wikipedia.org/wiki/File:Golden-Gate-Bridge.svg
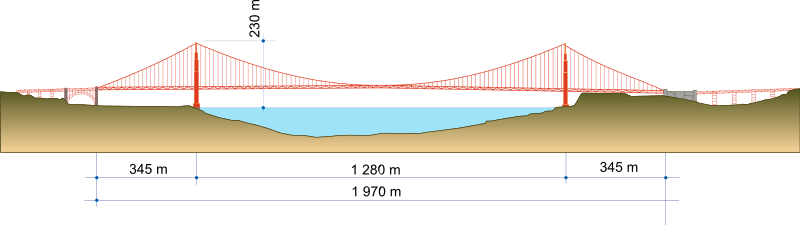
- El puente Golden Gate tiene dos grandes torres que soportan los dos cables principales.
- Altura de la torre por encima del agua: 230 m
- Altura de la torre por encima de la carretera: 150 m
Buruketa
Golden Gate zubiak San Frantziskon kokatzen da. Bere dorreek 150 metroko altuera dute errepidearen gainetik, eta haien artean 1280 metroko distantzia da. Dorreek 230 metroko altuera dute uraren mailaren gainetik. Kableek parabola bat osatzen dute eta galtzada ukitzen dute zubiaren erdian.
a) Zehaztu parabolaren ekuazioa.
b) Zehaztu zer altuera duten kableek galtzadarekiko, zubiaren erdigunetik kilometro erdi batera.
a) Zehaztu parabolaren ekuazioa
Parabolaren ekuazioa zehazteko, zubiaren erdian galtzada ukitzen duten parabolaren puntuak eta zubiko dorreen puntuen koordenatuak aurkitu behar ditugu.
Kableek parabola bat osatzen dutenez eta zubiaren erdian galtzada ukitzen dutenez, parabolaren ekuazioak forma hau du:
y = ax ^2 (0, 0) parabolaren erpina izanda
Parabolaren erpina zubiko bi dorreen arteko erdiko puntuan dago, 1280 metroko distantziaz banatuta. Beraz, zubiaren erdigunea x = 1280/2 = 640 m da.
Dorreek 150 metroko altuera dutenez eta 1280 metroko distantziaz banatuta daudenez, dorreetako baten koordenatuak har ditzakegu: (640, 150).
Parabolaren ekuazioan koordenatu horiek ordezkatuz, hau lortuko dugu: 150 = a · 640^2
Ekuazio hori ebatzita, "a" balioa aurkituko dugu: a= 0,0366
Beraz, parabolaren ekuazioa: y = 0,0366 x^2
b) Zehaztu zer altuera duten kableek galtzadarekiko, zubiaren erdigunetik kilometro erdi batera
Kableek galtzadarekiko duten altuera zehazteko, zubiaren erdigunetik 500 metrotara, x = 5 ordezkatu dezakegu parabolaren ekuazioan: y = 0,0366 · 5^2 = 91,55
Beraz, kableek galtzadarekiko duten altuera, zubiaren erdigunetik 500 metrora, 91,55 metrokoa da.