Un problema de áreas - opción 1
Un varilla de metal de 10m de largo se corta en dos partes como se ve en la figura de abajo. Cada pieza se dobla para formar un cuadrado. Encuentre una función que modele la "suma entre las áreas de los cuadrados que se forman"
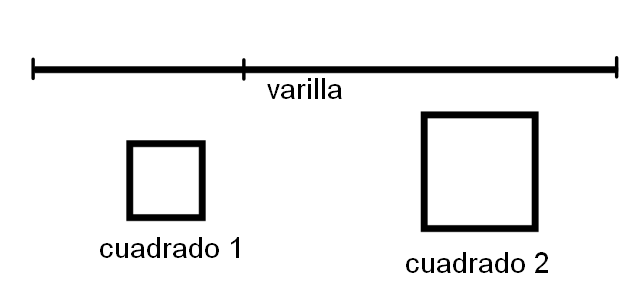
Si llamamos "x" a la longitud de una de las piezas en las que se corta la varilla. ¿Cómo podemos representar a la longitud de la otra pieza?
A partir de lo anterior..
Escribe una expresión que represente la longitud del lado del cuadrado 1 y otra que represente la longitud del lado del cuadrado 2.
Escribe una expresión que represente la "suma entre las áreas del cuadrado 1 y el cuadrado 2".
Contextualizando el problema en una construcción gráfica de Geogebra.
El siguiente applet muestra dos vistas gráficas.
A la izquierda: podemos observar cómo varía la suma entre las áreas de los cuadrados 1 y 2 en función de la longitud de una de las piezas "x".
A la derecha: podemos observar cómo varían cada una de las áreas de los cuadrados 1 y 2 por separado en función de "x". Notemos que "x" puede tomar valores entre 0 y 10.
El deslizador "a" representa el valor que puede tomar la variable "x".
Mueve el deslizador "a" y observa el comportamiento de las demás variables.
A PARTIR DEL APPLET DE ARRIBA, RESPONDE A LAS SIGUIENTES PREGUNTAS
¿Para qué rangos de "a" la suma de las áreas de los cuadrados 1 y 2 es menor a 4.25 m2 ?
¿Cuál es el valor de "a" que hace que la suma de las áreas sea mínima ?
¿Cuál es la suma de áreas mínima?
Evaluación
¿Qué te pareció la actividad?