Field and Current Layers in a synchronous machine with a smooth rotor
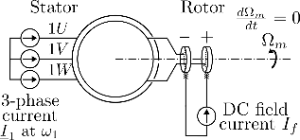
In this animation the stator (three phase symmetrical winding, phase width , terminals 1U, 1V and 1W) is fed by a controllable (in phase, frequency and amplitude) three phase current and the rotor (smooth rotor, distributed winding, phase width , terminals + and -) is fed by a DC current. The rotor speed follows from the stator frequency: with the number of pole pairs ( in the animation). is assumed so that the motor torque is always equal to the load torque : (i.e. only steady state conditions are animated).
Red and pink waveforms are the current densities and (A/m) of stator and rotor respectively. It is assumed that the phase conductors are spread very finely/thin over the phase width (), so that the current density is a constant over a phase width.
The black waveforms (dashed line) and (dash-dot line) are the accompanying mmfs (Aw) produced by the current densities and respectively (where and symmetry requirements allow to locate the neutral point where ). Please see also: https://www.geogebra.org/m/azhgwttv and https://www.geogebra.org/m/tny9ykfg.
The solid black line is the total mmf of rotor and stator, .
The torque resulting from a rotating fundamental field layer and rotating fundamental current layer can be calculated with . In this animation the reluctance of the iron core is neglected so that the air-gap induction in each point of the armature circumference follows directly from the local total mmf of rotor and stator: with and the air gap length. The torques and (produced by the fundamental functions) are given by (Nm): and with some (machine) constant. In the animation the torques are then given in relation to the maximum attainable torque in the animation (pu).
Field orientation can be achieved when:
- the fundamental parts of and are in phase, or
- the fundamental parts of and are in phase