La pendiente como una razón de cambio
Uno de los axiomas de formuló Euclides en lo que ahora denominamos Geometría Euclidiana, es que toda recta pasa por dos puntos. Esto implica que podemos determinar una recta dependiendo de cómo sean esos puntos.
Algo que podemos intentar observar de la recta es, cómo será su inclinación dependiendo de la separación que existe entre los dos puntos que la determinan.
Supongamos que tenemos dos puntos en el plano y ; pidamos que ambos puntos siempre estén separados a la misma distancia.
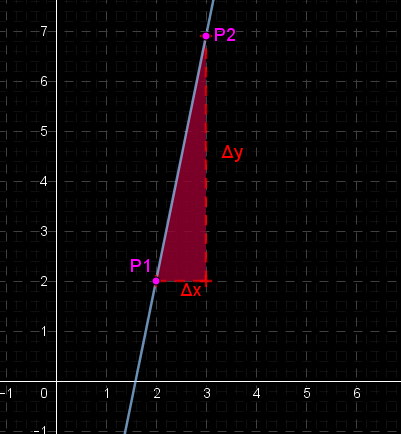
Observamos que, al colocar los puntos en el plano, éstos tendrán coordenadas que, cada una, estará separada cierta distancia de la otra.
Por ejemplo, en la imagen anterior, P1=(2, 2) y P2=(3, 7), así, podemos asegurar que P2 tiene como coordenada en x el valor de la coordenada en x de P1 aumentada en 1 unidad.
Diremos que el cambio en x corresponde a 1 y lo escribiremos , de forma análoga .
Observe que, en este caso, estamos leyendo el cambio de P1 a P2; tanto en "x" como en "y", las coordenadas aumentan, por lo que decimos que hay un cambio positivo, en caso contario, si disminuye, el cambio sería negativo y se utilizaría un número con signo para representarlo.
Dados los puntos A=(-4, 5) y B=(2, 9), encuentre y
Modifique el valor del cambio en "x" y observe lo que ocurre con el cambio en "y"
Notará que cuando aumenta, disminuye y viceversa, esto evidencia que existe una relación de proporcionalidad inversa entre estos cambios, definamos "pendiente" como la relación, .
Así, la inclinación de una recta se medirá por medio de la pendiente, tal que si es positiva, la recta tendrá inclinación hacia la derecha y si es negativa, hacia la izquierda.
¿Cuál será la pendiente de una recta que es completamente horizontal?
Cuando la recta que se trabaja es completamente vertical, decimos que la pendiente no está definida, ¿por qué?