Golden Section in math, art and nature
Music and Math
What is the link between Debussy's following musical composition and mathematics?
"Cathédrale Engloutie" is a prelude for piano of 89 bars, of which the first 68 have a double time of the remaining 21: in other words, at bar 68 the song slows down and the duration of the notes is halved. The effect produced upon listening, therefore, reduces the lines of this first section to 34, and the piece has a length perceived by the listener of 55 bars, namely the golden section of 89.
The golden section refers to the ratio between two unequal quantities of which the largest is the average proportional between the minor and their sum.
Expressed algebraically, for quantities and with ,
The value of this ratio is the irrational number
and it is also solution to the quadric equation:
.
The golden section, also called golden ration or golden proportion is frequently occurs in geometry, in fact there are polygons definable as golden polygons because they have golden ratios, for example the rectangle and the golden triangle.
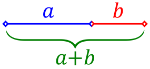
A golden rectangle is a rectangle whose side lengths are in the golden ratio.
Starting from the golden rectangles, we can construct an approximation of the golden spiral which is a particular logarithmic spiral that has growth factor with
that is the reciprocal of the golden number .
The parametric equation of the golden spiral is:
The following graphic represents the golden spiral.
By varying the parameter different spirals are obtained, we can observe that for the spiral will wrap counterclockwise, instead for will wrap clockwise.
Golden Rectangle and Approssimation of Golden Spiral
We can approximate the golden spiral through the construction of a succession of golden rectangles.
Algoritm:
1. Create a segment AB;
2. Create the golden section AG of AB using the method of Euclide (for example);
3. Build the rectangle ABGH;
4. Build another golden rectangle inside, describing the circumference of the center G and of the radius AG, finding its intersection I with the side GH and creating the segment IJ;
5. We can iterate the process, creating a total of 8 golden rectangles;
6. Draw the spiral through arcs of circumference.
It can be shown that the rectangles obtained are all golden rectangles and that the spiral obtained is a good approximation of the golden spiral.
Move the selector "c" to change the size of the AB segment and thus the size of first golden rectangle.
Fibonacci Spiral
The Fibonacci numbers are intimately linked to the golden section, in fact through them it is possible to find an algorithm to calculate as an approximation.
The Fibonacci numbers form a sequence such that each number is the sum of the two preceding ones, starting from 0 and 1. That is
,
and
, for .
It is shown that the limit of the Fibonacci sequence is the golden ratio .
In the following graphic succession of squares has been constructed whose sides are the Fibonacci numbers.
The first square and the second have side 1, the third has side 2, the fourth has side 3 etc.
Then rectangles with pairs of Fibonacci numbers as sides were constructed:
,
,
, for
Through arcs of circumference a spiral was obtained, called Fibonacci Spiral, which approximates the golden spiral well.
Moreover the table shows values of the sides of the rectangles and the ratios between the large sides and the small sides to observe that these ratios of the sides tend towards the golden number .
Golden Triangle
Another interesting polygon is the golden triangle.
A golden triangle is an isosceles triangle in which the duplicated side is in the golden ratio to the distinct side.
The following graphic represents a golden triangle.
Algoritm:
1. Build the golden section CH of the segment BC.
2. Find the third vertex of the triangle as intersection of the circumference of center H and radius CH and the circumference of center B and radius CH.
The table shows the values of the sides and the ratios to observe that they are in golden ratio.
Move the selector "b" to observe that, varying the dimension of the triangle, the ratios are always .
In the following graphic I would show how it is possible to construct an approximation of the golden spiral through a succession of golden triangles.
The table contains the sides and the ratios between the sides for the first, second and third constructed triangle, to show that the succession of triangles so constructed are golden. (similarly we can insert the measures related to the other triangles).
Move selector "b" to observe that changing the size of the triangles, the ratios remain equal to .
Dodecahedron and golden ratio
In this section I would like to show the close bond that links the regular polyhedra with the golden ratio, in particular for the dodecahedron.
The dodecahedron is a regular polyhedron with 12 pentagonal faces and its construction is repeatedly based on the golden section.
The centers of the twelve faces of the dodecahedron can be grouped into 4 to 4 to obtain 3 golden rectangles.
Algoritm:
We can show this in Geogebra in this way:
1. Build a dodecahedron starting by a pentagon.
2. Choose 4 pentagons (blue in the following graphic) :two adjacent and two opposite to the previous ones.
3. Find the center in each pentagon chosen
4. Consider the polygon that has these centers as vertices.
The obtained polygon is a golden rectangle, in fact the table shows that the ratio between the large side and the small side of the rectangle is .
Two other golden rectangles can be built inside the dodecahedron following the same procedure.
Golden ratio and Art
Very often it happens that in the works of different artists the presence of the golden section is found, especially in the form of a golden rectangle, for example in Greek architecture, in the construction of medieval churches, in Renaissance paintings.
Many Renaissance artists and mathematicians including Leonardo da Vinci, Piero della Francesca e Sandro Botticelli were very fascinated and inspired by the golden section.
With the golden section in his paintings, Leonardo discovered that, by looking at the works, a feeling of order could be created.
In particular, Leonardo incorporates the golden ratio into two of his masterpieces: "La Gioconda" and "Uomo Vitruviano".
![[i]"La Gioconda" of Leonardo da Vinci[/i]](https://www.geogebra.org/resource/wzugensd/svsKCx8U7qvEf6qv/material-wzugensd.png)
![[i]"Uomo Vitruviano" of Leonardo da Vinci[/i]](https://www.geogebra.org/resource/h3yb4hdx/SUzVr5IwUKlwCCmz/material-h3yb4hdx.png)
![[i]"Nascita di Venere" of Botticelli[/i]](https://www.geogebra.org/resource/sg3uvrba/5k02fBj7LIxzqVyN/material-sg3uvrba.png)
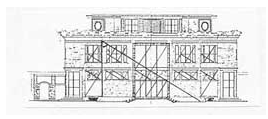
A particular attention to the golden section in the partition of the spaces is evident in some of the first works of the French architect Le Corbusier.
The regulatory paths that Le Corbusier marked on the drawing for the "Facade of Villa Schwob" in La Choux-de-Fonds are characterized by a central right triangle in which the relationship between the two sides is the golden number.
Golden spiral and nature
Also called "the eye of God", the golden spiral can also be traced in nature itself, in the shape of galaxies, in the biological growth of animal species, in the spacing between leaves along a stem, in the area of petals and seeds of sunflower, in the shells, up to the flight path and cobwebs of some insects.

Pedagogical Aspects
From the pedagogical point of view, it would be stimulating to bring young people closer to the study of the golden ratio through the creation of geogebra files.
In fact, through this graphic tool, they could understand more deeply a mathematical concept that seems so abstract.
Through the connection with works of art and naturalistic images they could be intrigued to investigate the topic and stimulated to look for golden spirals and golden sections in the world around them.
I insert two videos that could be used to stimulate students' attention in a playful way