Dokumentation Extremwertaufgaben
Einführung
Optimierungsprobleme begegnen uns im Alltag in der Industrie, Wissenschaft, Wirtschaft und im Privatleben. Da sie so eine wichtige Rolle spielen, werden sie auch im Mathematikunterricht, in der Form von Extremwertaufgaben behandelt.
Bei Extremwertaufgaben geht es darum, die optimale Lösung eines Problems, meistens Minima oder Maxima, zu bestimmen. in der fortgeschrittenen Schulmathematik werden diese Mithilfe der Differenzialrechnung bestimmt.
Wenn das Problem durch äußere Umstände (geometrische Einschränkungen, vorhandenes Material) eingeschränkt ist, so spricht man von Extremwertaufgaben mit Nebenbedingungen.
Bildungsplan
Extrema von Funktionen werden schon in Klasse 7/8 behandelt, im Rahmen von quadratischen Funktionen. Hier können Scheitelpunkte von Parabeln bestimmt werden, wodurch dann Anwendungsaufgaben mit Minima und Maxima behandelt werden können. Dabei kommen prozessbezogene Kompetenzen wie das Modellieren und das Lösen von Problemen zum Einsatz
In Klasse 9/10 wird die Differentialrechnung eingeführt und im Rahmen der Kurvendiskussion spezielle Punkte von Funktionen und ihren Graphen bestimmt. Dazu gehören auch Extrempunkte von jenen Funktionen, die im Rahmen von Extremwertaufgaben zum Einsatz kommen.
In der Oberstufe, also Klasse 11/12 behandelt man schließlich explizit Extremwertaufgaben mit Nebenbedingungen, wobei diese nur im Leistungskurs behandelt werden.
Einsetzungsverfahren
Extremwertaufgaben mit Nebenbedingungen werden typischerweise folgendermaßen gestellt: Eine Größe (z.B. Flächeninhalt, Volumen, Gewinn) soll maximiert bzw. minimiert werden, wobei sie durch äußere Umstände (geometrische Fläche, vorhandenes Material, Kostenfunktion) eingeschränkt werden. Um Sie zu lösen, schlagen der Lambacher Schweizer, sowie Elemente der Mathematik einen vorgefertigten Lösungsweg vor, das Einsetzungsverfahren:
1.Funktionsgleichung aufstellen
Zuerst werden alle relevanten Größen aufgestellt und eine Funktionsgleichung für den zu
optimierenden Wert aufgestellt. Dies ist die sogenannte Extremalbedingung. Auch eine Skizze
kann hilfreich zum Lösen des Problems sein
2. Nebenbedingungen aufstellen
Die Nebenbedingungen werden aus dem Text gelesen und mathematisch formuliert. Anschließend
werden die entstandenen Gleichungen so umgestellt, dass durch Einsetzen in die
Extremalbedingung alle Variablen bis auf eine eliminiert werden. Die entstandene Funktion, die nur
noch von einer Variable abhängig ist, nennt man Zielfunktion. Wichtig ist es auch, einen
geeigneten Definitionsbereich anzugeben, damit die Nebenbedingungen noch erfüllt werden.
3. Extremstellen finden
Die Zielfunktion wird abgeleitet und die Nullstellen der Ableitung bestimmt um die Extremstellen zu
finden. Durch einsetzen in die Zielfunktion erhält man schließlich die Extrempunkte. Eine
Randuntersuchung darf hier nicht fehlen.
4. Ergebnis formulieren
Am Ende wird das Ergebnis mit allen relevanten Größen angegeben und die Resultate am
Sachverhalt überprüft
Alternative Lösungswege
Das Einsetzungsverfahren ist die einzige Lösungsmethode die in den erwähnten Schulbüchern behandelt wird. Dass es aber manchmal andere, auch einfachere Lösungswege für solche Probleme gibt, soll folgendes Beispiel zeigen:
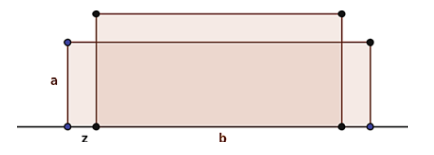
Aufgabe: Mittels zweier Pfosten und 100m Draht soll eine rechteckige Fläche eingezäunt werden. An einer Seite kann eine gerade Mauer als Begrenzung benutzt werden, auf die der Zaun senkrecht treffen soll. Der Flächeninhalt soll maximiert werden.
Dieses Problem kann mithilfe des eben beschriebenen Einsetzungsverfahrens gelöst werden, wobei die Extremalbedingung hier der Flächeninhalt ist. Die Nebenbedingung lautet und durch umstellen nach b und einsetzen in die Extremalbedingung erhält man die Zielfunktion . Durch die Ableitung erhält man die Extremstelle und durch einsetzen in die Zielfunktion ergibt sich der maximale Flächeninhalt zu .
Es gibt jedoch alternative Lösungswege zu dieser Aufgabe:
1. Scheitelpunktbestimmung
Bei der Zielfunktion handelt es sich um eine quadratische Funktion, der Graph ist also eine
umgekehrte Parabel. So kann man den maximalen Wert ganz einfach durch eine Scheitelpunkt-
Bestimmung ermitteln
2. Änderung des Flächeninhalts betrachten
Eine Vorgehensweise abseits der Analysis ist, sich das Änderungsverhalten des Flächeninhalts
anzusehen, wenn man bspw. die Seite a um die Länge verlängert. Damit die Nebenbedingung
erfüllt bleibt, so verkürzt sich die Seite b um . Im Umkehrschluss verliert man an den Seiten die
Fläche , während oben die Fläche hinzukommt. Der gesamte Flächeninhalt
vergrößert sich also, solange die Ungleichung erfüllt ist. Dies lässt sich
vereinfachen zu und da z beliebig größer 0 gewählt wurde ist eine Optimierung
möglich, solange gilt. Das unverbesserliche Optimum ist erreicht, wenn .
Durch bilden eines Gleichungssystems mit der Nebenbedingung erhält man die optimalen Werte
für a und b
3. Spiegeln an der Wand
Spiegelt man das Rechteck an der Wand, so reduziert sich die Aufgabenstellung auf das Problem,
von allen umfangsgleichen Rechtecken das mit dem größten Flächeninhalt zu finden, also ein
Quadrat.
Wie zu sehen ist, kann man solche Aufgaben auf verschiedene Art und Weise lösen, wobei auch nur mathematische Werkzeuge der Mittelstufe zum Einsatz kommen können. Es ist wichtig, dass bei vorhandener Zeit den SuS solche Lösungswege aufzuzeigen, damit sie Problemstellungen aus verschiedenen Blickwinkeln betrachten können.
Aspekte von Variablen
Einer der Hauptbestandteile von Extremwertaufgaben und generell der Mathematik sind Variablen. Da diese je nach Situation unterschiedliche Charaktere besitzen können, unterscheidet der Mathematiker Gunter Malle zwischenn drei Aspekten von Variablen:
1. Einzelaspekt
Hier wird die Variable als Platzhalter für eine bestimmte Zahl aus einem Zahlenbereich betrachtet.
Sie kann ausgerechnet, oder mit ihr gerechnet werden, wie in folgendem Beispiel die Variable x:
2. Simultanaspekt
Bei diesem Aspekt steht die Variable gleichzeitig für alle Zahlen eines Zahlenbereichs. Dieser wird
meistens bei Rechenregeln, Definitionen oder Beweisen verwendet. Er dient dazu allgemeine
Aussagen zu treffen, wie zum Beispiel bei den Binomischen Formeln
3. Veränderlichenaspekt
Beim Veränderlichenaspekt wird die Variable als veränderlich, bzw. variable auf einem
Zahlenbereich aufgefasst, was meistens bei Funktionen der Fall ist. In der Gleichung
durchlaufen die Variablen x und y den gesamten Bereich der reellen Zahlen, wobei x die freie und
y die abhängige Variable ist.
Variablenaspekte sind jedoch häufig nicht eindeutig festzulegen, weswegen es manchmal schwer ist zwischen ihnen zu differenzieren. Hat man ein Gleichungssystem mit mehreren Variablen, so stehen diese zunächst unter dem Simultanaspekt. Hat man es jedoch gelöst und jeder Variable wurde eine feste Zahl zugeordnet stehen sie unter dem Einzelaspekt.
Auch sind jene Aspekt stark vom Kontext abhängig. Betrachtet man beispielsweise die Formel für den Flächeninhalt , so stehen die Variablen a und b unter dem Simultanaspekt. Setzt man die Formel aber in den Kontext einer Aufgabe wie: "Wie verändert sich der Flächeninhalt wenn eine Seite verdoppelt und die andere verdreifacht wird?" So stehen sie unter dem Veränderlichenaspekt.
Parameter
Parameter sind eine spezielle Form von Variablen, die unter dem Einzelaspekt stehen. Sie sind oft in Funktionsgleichungen zu finden, unterscheiden sich vom Charakter jedoch stark vom Argument der Funktion, weswegen es wichtig ist, dass sie mit unterschiedlichen Vorstellungen verbunden werden. Dazu dient zum einen die sprachliche Unterscheidung, als auch ein konsequentes verwenden von den gleichen Buchstaben für Variablen mit den selben Vorstellungen.
So sind die Buchstaben am Anfang des Alphabets (a,b,c,...) oft mit dem Simultanaspekt verbunden, die Buchstaben am Ende des Alphabets(x,y,z,...) mit dem Veränderlichenaspekt und die Buchstaben in der Mitte des Alphabets, sowie Buchstaben mit Indizes (l,m,n,s,t,a_0,x_1) stehen eher unter dem Einzelaspekt.
Grenzen des Einsetzungsverfahrens
Das Einsetzungsverfahren, wie man es in der Schule lernt ist nur unter gewissen Vorraussetzungen anzuwenden:
1. Bei n Variablen müssen mindestens n-1 Nebenbedingungen existieren
2. Die Nebenbedingungen müssen eindeutig nach einer Variable umstellbar sein
Ist die erste Vorraussetzungen nicht erfüllt, so erhält man eine Zielfunktion, die von mehreren Variablen abhängig ist. Während das Problem auf Schulart nicht lösbar ist, so kann mit Hochschulwissen dennoch das Einsetzungsverfahren angewendet werden, indem die Differentialrechnung für den angewendet wird.
Ist jedoch die zweite Bedinung nicht erfüllt, so kann das Einsetzungsverfahren nicht angewendet werden und es muss auf andere Verfahren, wie z.B. das Lagrangeverfahren zurückgegriffen werden.
Extremwertaufgaben im Unterricht mit Geogebra
Mithilfe von Geogebra können Extremwertaufgaben mit Nebenbedingungen visuell sehr gut dargestellt werden. Während eine simple Skizze das Problem zwar verbildlicht, kann mithilfe der Funktion der zweiten Grafik bei Geogebra das Änderungsverhalten von Flächeninhalten und Graphen simultan dargestellt werden. Was das genau bedeutet, wird in folgendem Applet gezeigt:
In dieser Problemstellung, in der das Volumen eines Quaders innerhalb einer quadratischen Pyramide maximiert werden soll, kann mithilfe von Schiebereglern sowohl das Volumen des Quaders, als auch die Höhe und Grundfläche der Pyramide verändert werden. Wendet man diese an, so verändert sich gleichzeitig der Graph des Volumens, bzw. der Punkt auf dem Graph verschiebt sich mit dem Volumen des Quaders. Auch können Hilfestellungen und Lösungen ein- und ausgeblendet werden.
Solche Applets, die man in einfacherer Version auch leicht selbst erstellen kann, eignen sich hervorragend für einen Unterrichtseinstieg zu Extremwertaufgaben, oder dazu, die Lösung einer eher schwereren, im Unterricht behandelten Extremwertaufgabe zu verdeutlichen. Die Korrelation zwischen Graph und geometrischer Veränderung kann so SuS deutlich einfacher vermittelt werden.
