4. Fourier
Esta actividad pertenece al libro de GeoGebra Música y Matemáticas.
El problema de la cuerda vibrante se resiste
La causa de la confusión entre estos genios estriba en que los matemáticos de esta época concebían una función a modo de polinomio, es decir, lo que hoy llamamos función analítica. ¡Pero un polinomio queda perfectamente determinado para todos los valores una vez que se conocen sus valores en un intervalo por pequeño que sea!
Para ellos, el estado de vibración de una parte de la cuerda debería determinar la vibración de la cuerda entera.
Fourier
Fourier fue discípulo de Lagrange, Monge y Laplace. En su Teoría analítica del calor recurre a series trigonométricas para modelizar ciertos comportamientos evolutivos. Estas series permiten resolver, por fin, el problema de la cuerda vibrante, al servir de puente entre las sinusoidales de Taylor y las funciones generales de d’Alembert.


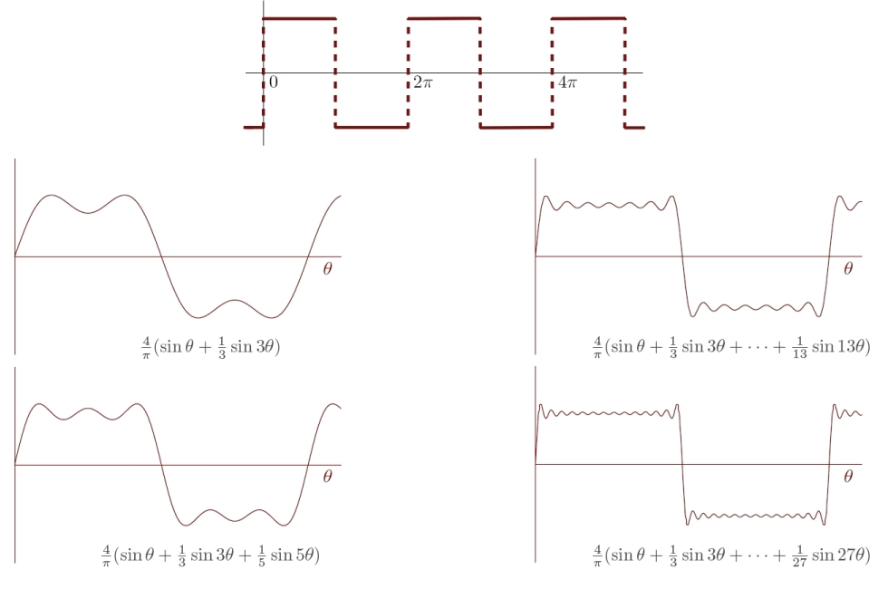
La gran diferencia entre la serie trigonométrica de Fourier y otras series, como la serie de potencias de Taylor, reside en que estas últimas representan una función analítica: toda ella está determinada por su comportamiento en cualquier pequeño intervalo. La serie de Fourier puede representar a una función mucho más general (como en el siguiente ejemplo) y tiene un carácter local: el valor de la serie en un entorno no contiene ninguna información sobre el valor de la serie en otro entorno disjunto del anterior.