3.3 Integral de línea para campos vectoriales gradiente
Integral de línea para campos vectoriales gradiente
Ahora, si se usara la integral de linea pero en vez de un campo escalar fuera un campo vectorial. Si imaginamos que estamos caminando sobre la trayectoria, a cada paso que damos tendríamos que hacer el producto punto de la curva tangente con el campo vectorial (el campo estaría evaluado en los parámetros de la curva), De esta manera obtendríamos la integral de lineal sobre un campo.
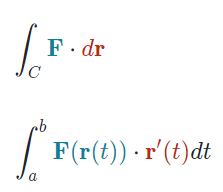
La diferencia entre la integral de linea entre un campo escalar y vectorial es que la tangente de la curva se esta tomando como eso, un vector en vez de que se tome como una distancia a diferencia de cuando ver aun campo escalar.
Se puede entender también esto como calcular el trabajo que hace una partícula al pasar sobre un campo vectorial
Teorema fundamental de las integrales de línea
Se podría decir que como las derivadas tiene una función inversa que es la integral, obtener el gradiente es una función que tiene su función inversa que es la integral de linea. De esta manera se puede ver la siguiente formula:
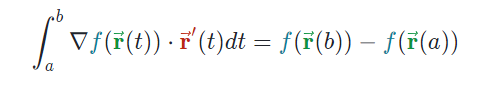
Quizá no es tan visible como es que sale esta formula pero al ver las propiedades del producto punto es que es visible ello y su relacion con el gradiente y la integral de linea.
En la siguiente grafica se podra observar ello