GeoGebra

Ray Tracing with Curved Mirrors

Author:Timo Budarz
When dealing with curved mirrors, there are three useful rays to track to find the resulting image location:
  1. A ray coming in parallel to the principal axis.
  2. A ray heading right for the center of the mirror where the surface is vertical like a plane mirror.
  3. A ray leaving the light source, passing through F, and reflecting parallel to the principal axis.
The first ray will pass through the focal point F (by definition) after reflecting, the second ray will go out at the same angle below the principal axis as in came in above the principal axis, and the third ray is essentially the reverse of the first ray. If the rays actually intersect as in the first picture, a real image is formed. Think of real images being formed by actual (real) light meeting. In contrast with real images, the second diagram shows that the rays will never meet since they are parallel. In this case no image is formed. In the last case the rays diverge after bouncing off the mirror. Remember what I mentioned above about tracing the rays back to their apparent point of origin. If we do this, it looks like the light came from some source on the right side of the mirror. Since the light seems to have come from that location, we will see an image there, but since it wasn't real light originating there, the image is called a virtual image.
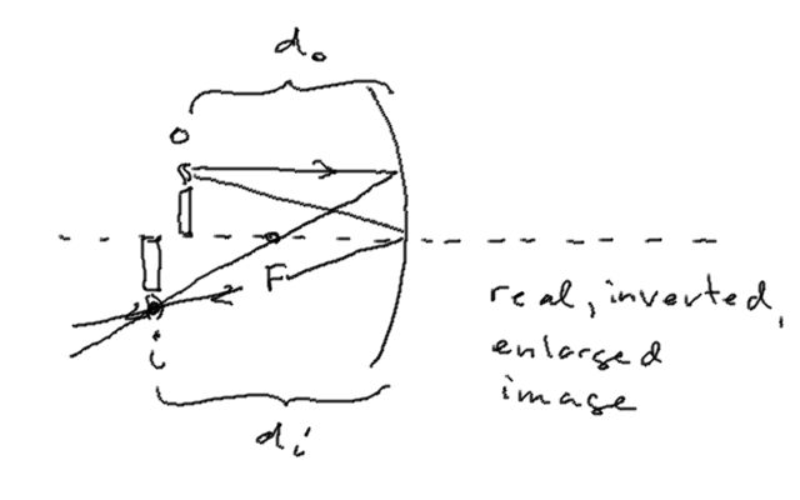
Image by Timo Budarz is in the Public Domain When an object is outside the focal point, a real image is formed with a concave mirror.
Image by Timo Budarz is in the Public Domain When an object is outside the focal point, a real image is formed with a concave mirror.
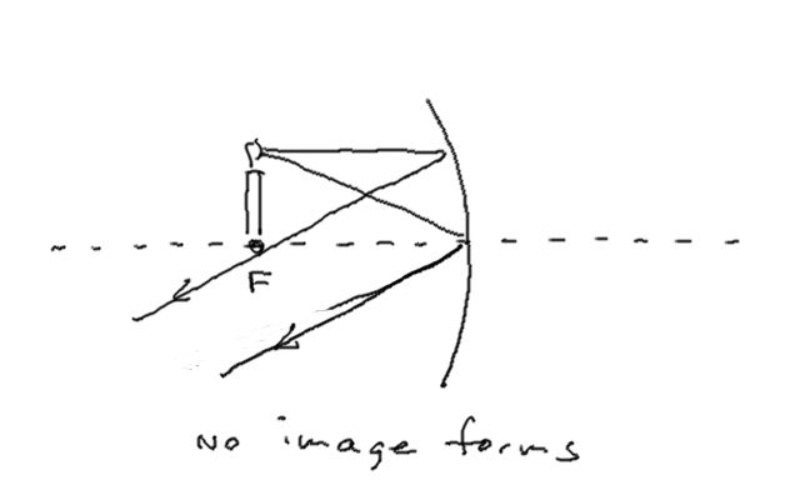
Image by Timo Budarz is in the Public Domain When the object is at the focal point, no image is formed.
Image by Timo Budarz is in the Public Domain When the object is at the focal point, no image is formed.
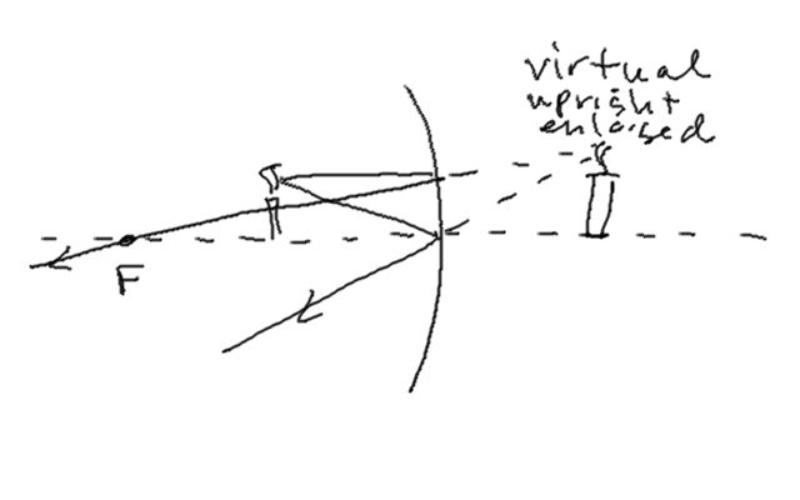
Image by Timo Budarz is in the Public Domain When the object inside the focal length of a concave mirror, a virtual image is formed on the opposite side of the mirror.
Image by Timo Budarz is in the Public Domain When the object inside the focal length of a concave mirror, a virtual image is formed on the opposite side of the mirror.

Sign Conventions

If we wish to label or measure the distances where the object sits and where the image forms, the rules are simple, and depend of what the light is doing.
    • First off, the object location is automatically considered positive and is typically drawn on the left side of the mirror or lens (like we read left to right).
    • The image distance is positive if it's a real image (made of real light) and negative if it's a virtual image.
    • Likewise, if the focal point is at a location where real light can go, the focal length is positive. It is negative if it's behind the mirror where light will never be.
    Obviously with a mirror the light will always stay on the same side as the object since it reflects. This is in contrast with lenses where the light passes through them and ends up on the other side.

    Image Location using Algebra

    The reason we care to place signs on these distances is that we need not always find images using diagrams. As you might suspect, there is an algebraic equivalent to these geometric drawings. There is an equation that goes by two names - the mirror equation and the thin lens equation - that relates the three quantities of object distance, image distance and focal length. Be sure to follow the sign conventions above. The equation is: Another useful equation is the magnification equation: This equation tells us how big the image is in relation to the object. When the magnitude of the magnification is greater than one, the image is larger than the object, and when it's smaller than one, the image is smaller. The sign of the magnification tells us whether the image is upright or inverted. Positive means an upright imagine, negative means an inverted image.

    New Resources

    Discover Resources

    Discover Topics