05-1 橢圓內的光線反射(試算表製作)
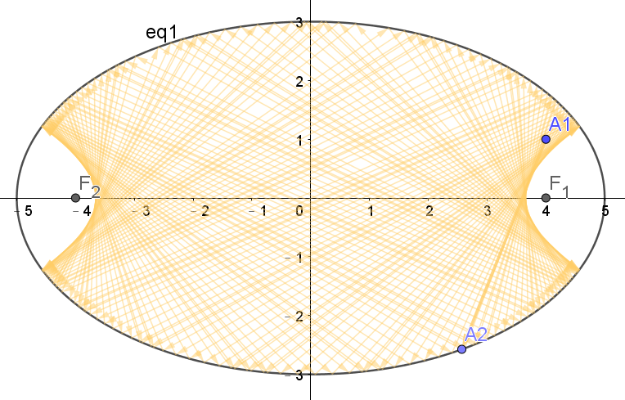
橢圓內的反射
如果用焦點來看,橢圓光線反射的光學原理,與拋物線上的光學原理不太一樣。但是反射的情況還是類似的,都可以藉著切線、法線來推得光線反射的路徑。
而橢圓內的反射,我覺得是比拋物線上的反射有趣。就無限次反射的情形下,拋物線上的光線反射可能反射個幾次,就會超出我們的視線範圍;不過橢圓內的反射就永遠囿於橢圓之中,所有的反射的情形都可以看得到。而且大多時候,當反射次數夠多,累積的反射路徑就會變成橢圓或雙曲線的包絡線。
因為反射還是與切線、法線有關,所以之前用來製作拋物線反射的方法,可以直接用來製作橢圓內的反射。
在此處製作 橢圓上的光線反射(試算表製作)
步驟1 製作橢圓與打開試算表
(1) 在指令列輸入指令:x^2 /25 + y^2 /9 = 1 (長軸長10,短軸長3的橢圓)
(2) 在"檢視"之中,打開試算表視窗
步驟2 製作光源起點A,以及最初的反射點B
.確認一下橢圓的名稱是否為eq1,以下以橢圓名稱為eq1為例去操作
(1) 在橢圓內部製造一新點A。
(2) 在橢圓上製造一點B。
(3) 製作向量AB,作為光線的示意。
步驟3 製作橢圓在B點上的法線
.相較於切線,實際上更重要的是法線。
.這裡就不再另外製造出切線,而是將切線放入雙重指令。
.製作法線:輸入指令PerpendicularLine(B, Tangent(B, eq1) ),得到直線g。
步驟4 製作反射光線
(1) 做點A對法線g的對稱點A',可用線對稱工具或者指令Reflect(A, g)。
(2) 做出射線,輸入指令Ray( 0.99*B+0.01*A' , A' )。
(3) 做出射線與橢圓eq1的交點,得到C點。
步驟5 將物件放入試算表
(1) 將點更名:A→A1、 B→A2、 C→A3、 。
(2) 將過點A2(原本的點B)的法線,更名為B2 。
(3) 將點A1(原本的點A)的反射點A',更名為C2 。
(4) 將射線更名為D2 。
(5) 將向量A1A2(原本的向量AB)更名為E2。
更名之後,物件就會被放到試算表之中
步驟6 隱藏不必要物件
隱藏不必要出現的法線、對稱點和射線。
而試算表之中的B,C,D欄,即是製作過程中,所製造出來的法線、對稱點和射線。
利用試算表的特性,將B,C,D欄全部框起來之後,將其物件隱藏。
PS:這裡我們先隱藏再作複製,是因為此次要複製出近千個物件,先將其隱藏,比較不會造成視覺上的混亂,也比較不會造成程式的負擔。
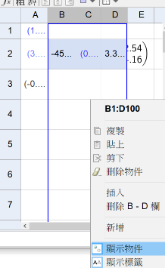
步驟6 利用試算表特性,複製指令
參考下圖操作
(1) 在試算表上框起B2:E2,並將其複製到B3:E3 。
(2) 接著在試算表上框起A3:E3,複製到A201:E201 。
如此,便能快速增加近199次的反射模擬。
PS:預設的試算表只有100列,必須先手動點擊第100列的任一儲存格,
再按住鍵盤的方向鍵"↓",就會快速擴展儲存格的列數。
不需要調整特殊情形
橢圓內的反射,並不像拋物線在射過焦點之後會反射到無限遠處(無下一個反射點),所以不需要再另外調控射線的顯示與否。