Círculos
Circunferencia
Antes de definir los círculos, debemos hablar sobre la circunferencia.
Llamamos circunferencia a una línea curva, formada por una cantidad infinita de puntos, alrededor de un punto central al cual equidista cualquier punto en la curva.
Círculo
El círculo se define por la figura plana que se encuentra dentro de la circunferencia.
Elementos del círculo
A continuación, definiremos e ilustraremos los siguientes conceptos:
- Centro
- Radio
- Diámetro
- Arco
- Cuerda
- Recta Tangente
- Recta Secante
Centro
El centro de un círculo es el punto al cual equidistan todos los puntos en la circunferencia.
En la figura anterior, el punto es el centro del círculo
Radio
Llamamos radio a todo segmento que une el centro del círculo con cualquier punto en la circunferencia.
Observen el radio OB en la siguiente figura:
Diámetro
El diámetro es el segmento de mayor longitud en el círculo. Une a dos puntos de la circunferencia y pasa por el centro del círculo.
Observemos el siguiente diámetro AB que pasa por O.
Arco
Llamamos arco a una parte de la circunferencia de la figura.
En la siguiente figura, notaremos el arco AB como la parte más corta de la circunferencia entre los puntos A y B
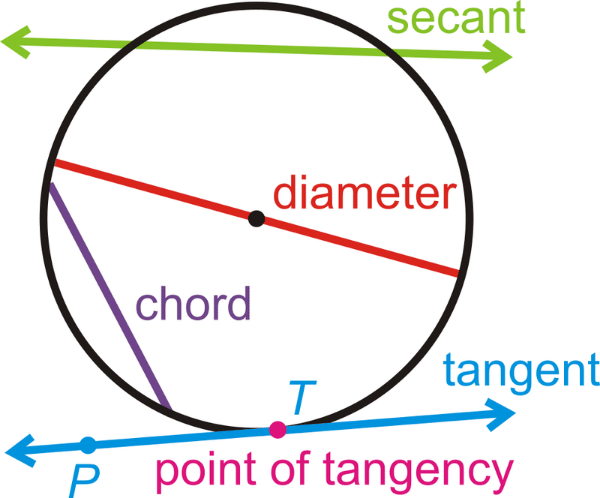
Cuerda
Llamamos cuerda al segmento que une dos puntos en los extremos de un arco.
En la figura anterior, el segmento AB es una cuerda.
Recta Tangente
La recta tangente es una recta que toca a la circunferencia en un solo punto. Este punto se le conoce como el punto de tangencia.
Una propiedad importante de la recta tangente es que el radio de O hasta el punto de tangencia es perpendicular a la tangente.
Recta Secante
Una recta secante atraviesa el círculo en dos puntos distintos en la circunferencia.
Semicírculo, Sector circular, segmento circular.
El semicírculo es la parte que resulta al dividir el círculo con el diámetro.
El sector circular se determina por la parte del círculo entre dos radios y su arco
El segmento circular es determinado por una cuerda y su arco.
Area del círculo
El área del círculo es determinado por:
Fuente de información: https://planificacionturbo.com/static/leccion/teoria/1467905160008.pdf
Teorema de la barquilla
Si trazamos dos rectas tangentes a una circunferencia desde un punto P, entonces los segmentos de recta desde P a los puntos de tangencia son iguales y el centro de la circunferencia yace en la bisectriz del ángulo entre las rectas.
Demostración: Sea una circunferencia con centro O y un punto P fuera de la circunferencia.
Tomemos los puntos en la circunferencia A y B tales que PA y PB sean tangentes de la circunferencia.
Notamos que los triángulos OBP y OCP son triángulos rectángulos que comparten un lado (OP). Como OB y OC son radios, entonces son iguales. Por Pitágoras, tenemos que PB=PC. Entonces ambos triangulos son congruentes (LLL). Al ser congruentes, es decir que O se encuentra en las bisectriz del ángulo BPC.
Teorema de puntos y c
Dado tres puntos no colineales, siempre existe un círculo que pasa por los tres puntos.
Demostración: Tomemos tres puntos no colineales A, B, y C. Sea O el punto en donde las mediatrices de AB y BC se cortan (ya que son no colineales, se intersecarán en algún punto).
Como O está en la mediatriz de AB, entonces O equidista a A y a B. Como O está en la mediatriz de BC, entonces O equidista a B y a C. Por lo tanto, A, B, y C están en la circunferencia con centro O y radios OA, OB, y OC (todos iguales).