3.3 Como calcular a distância no plano
Introdução
O objetivo dessa apresentação é descobrir como calcular a distância entre ponto genérico A e uma reta qualquer r no plano cartesiano, que chamaremos de D(A,r).Vale lembrar que quando falamos de distância entre ponto e reta nos referimos à MENOR distancia entre elas.
Teoria
A demonstração de como é calculada a distância entre uma reta e um ponto é basicamente a mesma da apresentada no caso geral que é a do espaço, que foi demonstrada na apresentação anterior. Porém, por se tratar de elementos no plano cartesiano tem como simplificar ainda mais a fórmula final, o que deixa a resolução desse tipo de exercício mais fácil.
Sabe-se que
D(A,r)= Distância do ponto A à reta r
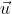=vetor PA
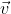=vetor diretor da reta
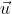Área do paralelogramo(por meio de produto vetorial): || X ||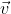
Área do paralelogramo(pela fórmula): ||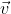|| * h
Assim, já que ambas as áreas tratam do mesmo paralelogramo, é possível relacioná-las:
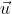|| X 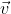|| = ||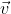|| * h
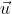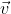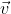Finalmente: h=D(A,r)= || X || / |||| = ||
X || / ||||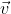
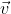Essa é a equação geral que vale tanto para o espaço, quanto para o plano, mas por se tratar de uma dimensão mais simples é possível dar uma nova cara à essa fórmula.
Equação cartesiana da reta r : 
=0
Ponto A=
Por meio de algumas operações matemáticas, temos que ||X || =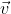
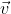Sabemos que |||| = . (Embora o vetor (a,b) seja na realidade o vetor normal à reta, eu posso usá-lo porque o módulo deles é o mesmo)
Logo, a equação da distância entre ponto e reta no plano:
h=D(A,r)= /