Μεσοπαράλληλος
Έργο 1
Στο παρακάτω σχήμα οι ευθείες ε1, ε2 και ε3 (φούξια ευθείες) είναι παράλληλες. Η ευθεία δ1 τις τέμνει και όπως βλέπετε οι τρεις φούξια ευθείες ορίζουν στην δ1 ίσα τμήματα (τα μπλε τμήματα ΑΒ και ΒΓ). Η ευθεία δ2 είναι μια άλλη ευθεία που τέμνει τις τρεις παράλληλες.
Μετακινήστε τα σημεία Δ, Ε όπως θέλετε. Τι παρατηρείτε για τα τμήματα ΔΕ, ΕΖ;
Μπορείτε να διατυπώσετε ένα θεώρημα;
--------------------------------------------------------------------------------------
Έργο 2
Στο παρακάτω σχήμα οι ευθείες ε1 και ε2 είναι παράλληλες. Τα σημεία Α και Β βρίσκονται ενδιάμεσα των δύο παραλλήλων. Στο σχήμα αναγράφονται οι αποστάσεις των σημείων Α και Β από την ευθεία ε1 (με μπλε χρώμα) και από την ευθεία ε2 (με κόκκινο χρώμα).
Μετακινήστε τα σημεία Α, Β έτσι ώστε να ισαπέχουν από τις ευθείες ε1 και ε2. Τι συμπεραίνετε για την ευθεία που ανήκουν τα σημεία Α και Β (γκρι ευθεία);
--------------------------------------------------------------------------------------
Έργο 3
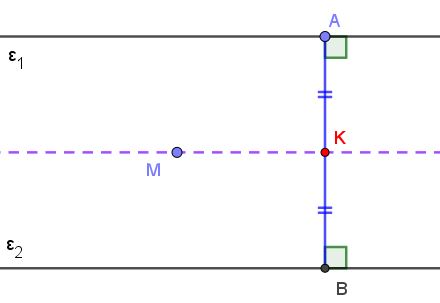
Στο παρακάτω σχήμα οι ευθείες ε1 και ε2 είναι παράλληλες. Από σημείο Α της ευθείας ε1 φέρνουμε κάθετη στην ε1 (μπλε ευθεία), η οποία θα είναι προφανώς κάθετη και στην ε2. Ονομάζουμε Β το σημείο τομής της κάθετης ευθείας (της μπλε δηλαδή) με την ευθεία ε2.
Στο ευθύγραμμο τμήμα ΑΒ που προκύπτει παίρνουμε το μέσον Κ (κόκκινο σημείο).
Επομένως το Κ ισαπέχει από τις ευθείες ε1 και ε2.
Μετακινήστε το σημείο Α και δείτε τις πιθανές θέσεις του σημείου Κ. Τι συμπεραίνετε;
Η ευθεία που είδατε να εμφανίζεται στο προηγούμενο σχήμα καλείται μεσοπαράλληλος των ε1, ε2.
Ορισμός
Θεωρούμε τις παράλληλες ευθείες ε1 και ε2 και ένα τμήμα ΑΒ κάθετο προς αυτές (όπως στο παρακάτω σχήμα). Αν Κ είναι το μέσον του ΑΒ τότε η παράλληλη από το Κ στις ευθείες ε1 και ε2 ονομάζεται μεσοπαράλληλος των ε1, ε2.
Μπορείτε να αποδείξετε ότι η μεσοπαράλληλος δύο παράλληλων ευθειών ε1 και ε2 είναι ο γεωμετρικός τόπος των σημείων που ισαπέχουν από τις δύο ευθείες;