Thalesz tétel
Bizonyítás
A háromszögek szögösszegtétele alapján
Azt fogjuk felhasználni, hogy a háromszög belső szögeinek összege 180°.
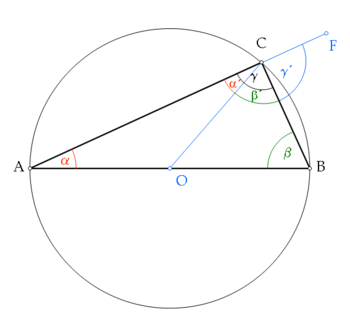
Legyen O a kör középpontja. Ekkor az AOC és a COB háromszög egyenlő szárú, azazα = α' ésβ = β'.
Az OC szakasz pont az α' és β' részekre osztja γ-t , így
γ = α' + β' = α+β
Az ABC háromszög belső szögeinek összege (ami a szögösszegtétel szerint 180°) épp e négy szög összege, tehát:α + β + γ = α + β + (α' + β') = α + β + (α + β) = 180°;
vagyis:2α+2β = 180°2(α+β) = 180°α+β = 90°így:γ = α + β = 90°
Eukleidész bizonyítása
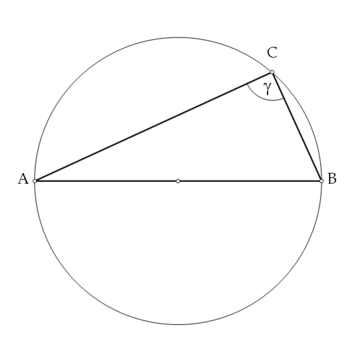
Azt kell belátnunk, hogy az ábrán a γ szög hegyesszög vagy derékszög.
Hosszabbítsuk meg az AC szakaszt C-n túl egy tetszőleges F pontig.
Legyen O a kör középpontja. Mivel AO és OC a kör sugara, ezért az AOC háromszög egyenlő szárú, ígyα = α'.
Továbbá, mivel OB is a kör sugara ezért az OBC háromszög is egyenlő szárú, ígyβ = β'.
Mivelγ = α' + β',ezért az előbbiek miattγ = α + βis teljesül.
Viszont a külsőszög-tétel miatt az ABC háromszög γ' külső szöge egyenlő a két nem mellette fekvő belső szög összegével, azazγ' = α + βvagyisγ = γ'amiből az következik, hogy γ fele az egyenesszögnek, tehát C-nél derékszög van.
Egy elemi geometriai bizonyítás szimmetriatulajdonságokkal
Rajzoljuk be az O középpontot és hosszabbítsuk meg a CO szakaszt O-n túl a kör ívéig, amit metsszen a D pontban.
Azt kell belátnunk, hogy a C-nél lévő szög derékszög.
Tudjuk, hogy egy négyszög akkor és csak akkor téglalap, ha átlói felezik egymást és egyenlő hosszúságúak. De az ADBC négyszög átlói egyenlők (mert mindkettő a kör átmérője) és felezik egymást (az Opontban), így az ADBC négyszög téglalap.
Ebből viszont következik, hogy minden szöge, így a C-nél lévő szög is derékszög.
Megjegyzés.
Természetesen a szimmetriát itt az O pontra vonatkozó középpontos tükrözés jelenti.
A Pitagorasz-tételből és megflordításából
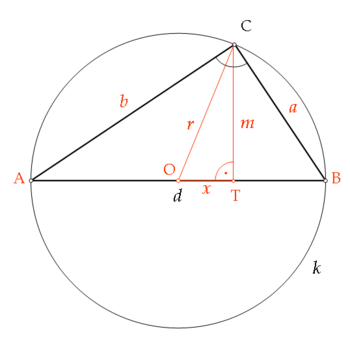
Legyen a k kör egy átmérője d, középpontja O. Vegyünk föl a kör ívén egy, az átmérő két végpontjától
különböző C pontot és bocsássunk merőlegest C-ből d-re. Legyen a merőleges talppontja T.
Az OTCderékszögű háromszög oldalait jelöljük így:
r = OC (a kör sugara)m = TC (az ABC háromszög C-ből kiinduló magassága)x = OTTovábbáa = BC ésb = AC
Ekkor az OTC, ATC és CTB derékszögű háromszögekre rendre felírhatjuk a Pitagorasz-tételt:x2 + m2 = r2(r + x)2 + m2 = b2(r – x)2 + m2 = a2
Azt fogjuk belátni, hogy az ABC háromszög olyan, hogy két oldalának négyzetösszege egyenlő a harmadik négyzetével ( a2 + b2 = d2 ).
A Pitagorasz-tétel megfordítása szerint ugyanis ekkor ABCderékszögű háromszög (és a derékszög a d-vel szemközt van).a2 + b2 = (r – x)2 + m2 + (r + x)2 + m2 = r2 -2rx + x2 + m2 + r2 + 2rx + x2 + m2 = 2r2 + 2x2 + 2m2 = 2r2 + 2(x2 + m2) = 2r2 + 2r2 = 4r2 = (2r)2 = d2Tehát a C-nél lévő szög derékszög
.Megjegyzés. Az O = T esetben a tétel triviális módon igaz, hiszen ekkor az AOC és az OBC háromszögek egybevágó egyenlő szárú derékszögű háromszögek. Ekkor tehát γ = 45° + 45° = 90°.