Introduzione
Il problema di determinare l’area di una superficie dal contorno curvilineo è stato affrontato sin dall’antichità, ad esempio le popolazioni dell'Egitto dovevano ricalcolare gli appezzamenti di terreno dopo le esondazioni del Nilo.
Si parla anche di quadratura poiché l’obiettivo è trovare un quadrato equivalente alla superficie della
quale vogliamo calcolare l’area.
Un approccio sistematico e rigoroso (ovvero "matematico" con l'accezione che diamo noi oggi a questo termine) avviene nella Grecia antica con apporti di numerosi studiosi nel corso dei secoli; tra questi occorre ricordare Archimede di Siracusa (287-212 a.C.) che recuperò e potenziò il metodo di esaustione (già
proposto da Antifonte 430 a.C.), tale metodo consiste nella costruzione di una successione di poligoni
che convergono alla figura data.
Il problema di quadrare alcune superfici chiuse, ad esempio il cerchio, sin dall'antica Grecia ha assunto un ruolo centrale tanto nella cultura greca quanto nelle culture successive fino ad arrivare al XIX secolo.
Il problema della “quadratura del cerchio” (ovvero il calcolo dell’area del cerchio) diviene paradigma (esempio, modello) a volte idealizzato e mitizzato; il nodo centrale risiedeva nel cercare una soluzione al problema con il solo utilizzo della “riga e compasso” -ovvero oggi diremmo con i soli numeri razionali, le operazioni aritmetiche e le radici quadrate.
Tale problema non ha soluzione (verrà dimostrato solo nel XIX secolo) ma ha permesso di creare/scoprire numerosi risultati di matematica nel corso dei secoli.
Ancor oggi nel parlare quotidiano si usa “quadrare il cerchio”.
Nell'introdurre l'integrale definito abbiamo osservato che corrisponde alla somma algebrica S delle regioni piane delimitate dal grafico della funzione e dalle rette e e dall'asse delle ascisse.
Per chiarire .
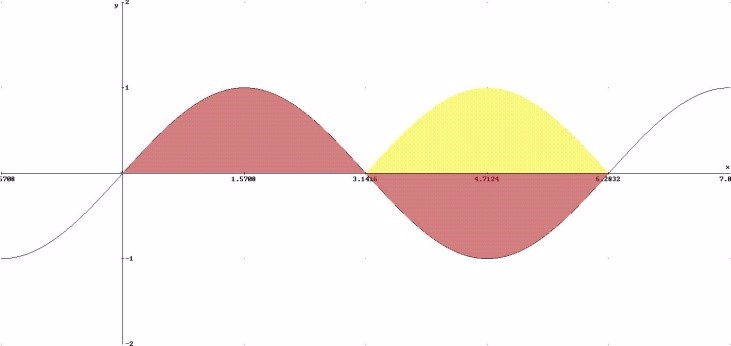
Infatti con riferimento alla figura in basso corrisponde alla somma algebrica delle due aree in rosso (quella tra risulterà positiva, mentre in risulterà negativa).
Se vogliamo calcolare l'area della regione delimitata dall'asse x e dalla funzione allora dobbiamo sommare alla regione in il valore assoluto del valore calcolato con corrispondente alla zona in giallo.
Equivalentemente osserviamo che e corrisponde al bordo della zona gialla in figura.