Die Scheitelpunktform
Die Eigenschaften einer Parabel: Ablesen aus dem Funktionsgraphen.
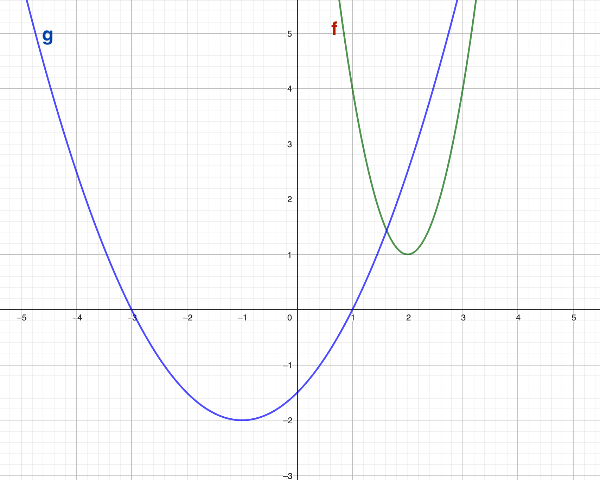
Die Beschreibungen der Eigenschaften der Parabeln.
Korrigiere, falls es nötig ist. Parabel f: Die Parabel f ist eine gestreckte Parabel, die um eine Einheit nach rechts und um eine Einheit nach oben verschoben ist. Der Scheitelpunkt liegt bei . Da sie nach unten geöffnet ist, besitzt f keine Schnittpunkte mit der x-Achse. Parabel g: Die nach oben geöffnete Parabel g besitzt einen Schnittpunkt mit der x-Achse. Sie ist gestaucht und um zwei Einheiten nach unten verschoben. Da sie auch um eine Einheit nach links verschoben ist, ist der Scheitelpunkt der Parabel bei .
Die Parametereinflüsse im Überblick
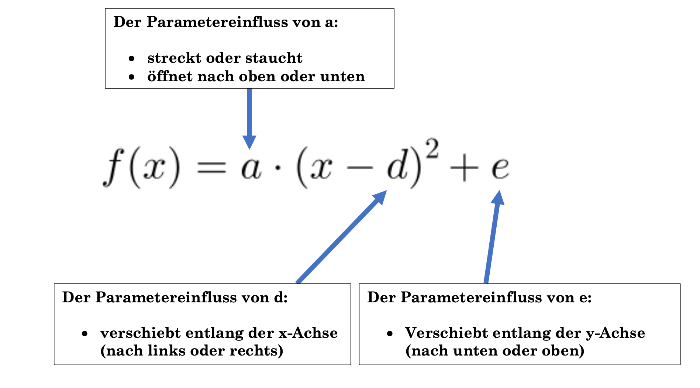
Die Beschreibung einer Parabel anhand der Funktionsgleichung
Wir haben die Scheitelpunktformen der Parabeln und gegeben. Beschreibe die Eigenschaften der Parabeln. Zusatz: Gib an, wie viele Schnittpunkt die Parabeln mit der x-Achse besitzen.
Überlege dir, welcher der Punkte die Scheitelpunkte zu den Funktionsgleichungen sind.
Gib deine Ergebnisse aus der vorigen Aufgabe hier an.