Chancen und Risiken digitaler Werkzeuge (Dokumentation)
Einleitung
Digitalisierung. Ein Wort, dem in den letzten Jahren vor allem durch die Corona Pandemie wieder mehr Bedeutung und Beachtung zuteil wurde. Nicht zuletzt aufgrund der Tatsache, dass die Einschränkungen durch die Pandemie aufgezeigt haben, wie es um den "Digital-Standort Deutschland" bestellt ist. In diesem Zusammenhang wurde außerdem deutlich, dass auch das deutsche Schulsystem großen Nachholbedarf bei der Digitalisierung aufweist. Wer sich mit dem Thema Digitalisierung im Kontext Schule befasst, kommt unweigerlich mit dem Begriff "digitale Werkzeuge" in Kontakt. Neben dem Online-Unterricht eignen sich digitale Werkzeuge aber insbesondere für den normalen Schulalltag in Präsenz, auch wenn sie hier häufig stiefmütterlich behandelt werden. Die folgende Dokumentation soll nach einer kurzen Systematisierung des Feldes digitaler (Mathematik-)Werkzeuge und einer Einführung in die Bedeutung von Repräsentationsformen für den Matheunterricht, aufzeigen, an welcher Stelle sich der Bildungsplan des Landes Baden-Württemberg zum Einsatz digitaler Werkzeuge im Matheunterricht äußert. Im Anschluss soll der Einsatz der dynamischen Geometriesoftware GeoGebra an dem Lerngegenstand der Sinusfunktion erprobt werden.
Was versteht man eigentlich unter digitalen Werkzeugen?
Im Zusammenhang mit digitalen Werkzeugen kursiert eine Vielzahl unterschiedlicher Begriffe, welche teilweise gleichbedeutend verwendet werden, sodass zuerst eine Systematisierung des Begriffs notwendig wird. Diesbezüglich bietet sich die Unterscheidung zwischen Lernumgebung und Werkzeugen an (vgl. Barzel et al., 2005, zitiert nach Thurm, 2020, S.11). Dabei wird unter einer Lernumgebung all das verstanden, was den Lernenden von außen instruiert (Ziele, Inhalte, Kommunikationsformen usw.) während Werkzeuge universell einsetzbare Hilfsmittel darstellen, welche zur Bearbeitung einer breiten Klasse von Problemen dienen (vgl. ebd.). Bei Letzteren wird eine Unterscheidung zwischen klassischen Werkzeugen (z.B. Geodreieck, Zirkel, Lineal usw.), allgemeinen digitalen Werkzeugen (z.B. Textverarbeitungsprogramme) und digitalen Mathematikwerkzeugen mit einer besonderen Relevanz für die Mathematik (z.B. dynamische Geometrie Software) vorgenommen (ebd.).
Es ist allerdings zu beachten, dass diese Unterscheidung zwischen Lernumgebung und digitalen Werkzeugen nicht trennscharf ist, da bspw. von einer Lehrperson interaktive Arbeitsblätter erstellt werden können, die den Einsatz digitaler Werkzeuge einfordern, oder aber direkt in ein digitales Werkzeug implementiert sind. Auf diese Weise gibt es keine klare Grenze mehr zwischen der Lernumgebung und dem Werkzeug.
Repräsentationswechsel
Ein grundlegendes Problem von Mathematik ist, dass mathematische Objekte in der Regel sehr abstrakt sind, da man sie weder mit dem Auge sehen, noch ein Bild von ihnen aufnehmen oder unter einem Mikroskop studieren kann. Um einen Zugang zu erhalten müssen wir mit Zeichen, Symbolen, Ausdrücken, Skizzen usw. arbeiten (vgl. Duval, 2000, zitiert nach Thurm, 2020, S.13). In diesem Zusammenhang spricht man in der Fachliteratur von unterschiedlichen Darstellung- bzw. Repräsentationsformen. Um mathematische Objekte zu verstehen und den Umgang mit ihnen zu erlernen kommt den Repräsentationsformen und dem Wechsel zwischen ihnen eine besondere Bedeutung zu. An dieser Stelle können digitale Mathematikwerkzeuge einen besonderen Mehrwert liefern, da sie bspw. die Möglichkeit liefern zwischen verschiedenen Darstellungsformen schnell und mit geringem Aufwand zu wechseln. In GeoGebra kann z.B. mit wenigen Befehlen innerhalb kürzester Zeit in einem Fenster gleichzeitig der Funktionsgraph inkl. seiner Funktionsvorschrift und einer Wertetabelle angezeigt werden.
![Abb. 1: Funktionsgraph der Funktion [math]f\left(x\right)=2^x[/math] mit einer Wertetabelle](https://www.geogebra.org/resource/ddquke7w/FPeHdo2TazbV0OjB/material-ddquke7w.png)
Diese Erkenntnis spiegelt sich auch in den Ergebnissen der Kultusministerkonferenz wieder. Dort heißt es: "Die Entwicklung mathematischer Kompetenzen wird durch den sinnvollen Einsatz digitaler Mathematikwerkzeuge unterstützt. Das Potenzial dieser Werkzeuge entfaltet sich im Mathematikunterricht [...] durch Verständnisförderung für mathematische Zusammenhänge, nicht zuletzt mittels vielfältiger Darstellungsmöglichkeiten [...]" (2012, S.13).
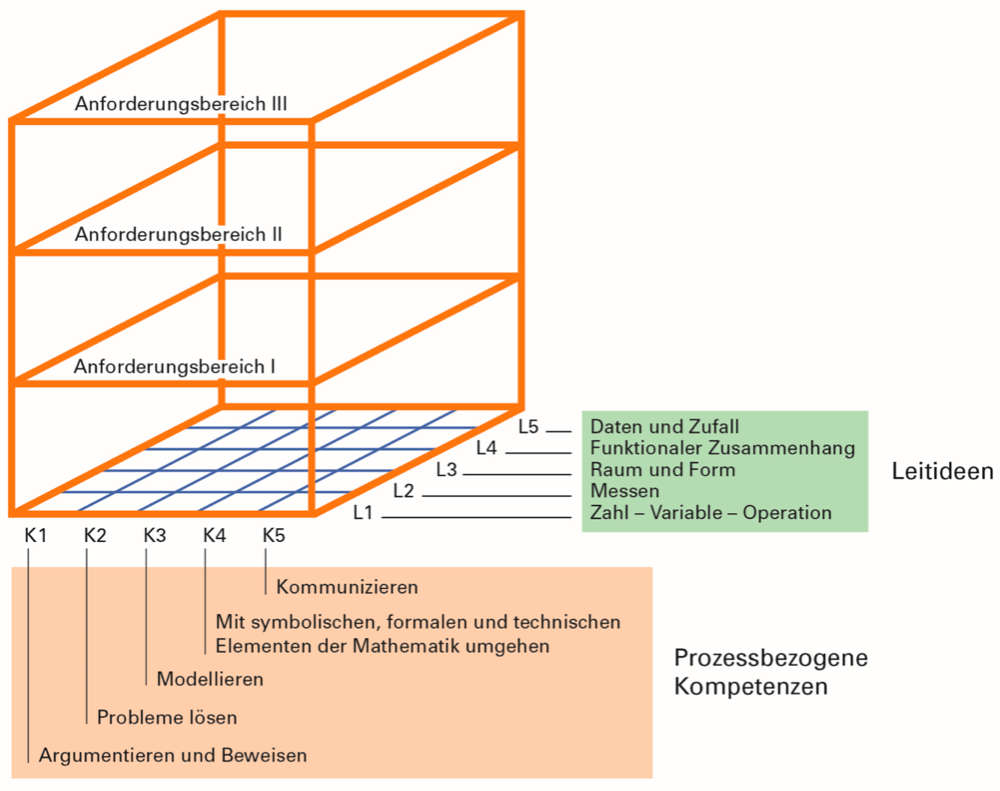
Bildungsplan - Kompetenzen
In dem Bildungsplan des Landes Baden-Württemberg für das Fach Mathematik an Gymnasien aus dem Jahr 2016 spielen mathematische Kompetenzen eine zentrale Rolle bei der Wissensvermittlung bzw. dem Wissenserwerb. Auch hier findet sich bei den prozessbezogenen Kompetenzen unter K4 "Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen" der Bezug zu den unterschiedlichen Repräsentationsformen.
Konkreter heißt es dort: "Die Schülerinnen und Schüler können [...] mathematische Darstellungen zum Strukturieren von Informationen, zum Modellieren und zum Problemlöser auswählen und verwenden [und] zwischen verschiedenen mathematischen Darstellungen wechseln" (Bildungsplan, 2016, S.13). An einer anderen Stelle wird in diesem Zusammenhang außerdem erwähnt, dass die Schülerinnen und Schüler "[...] Taschenrechner und mathematische Software (Tabellenkalkulation, Dynamische Geometriesoftware) bedienen und zum Explorieren, Problemlösen und Modellieren einsetzen [können sollen]" (ebd.).
Vorwissen
Die Schülerinnen und Schüler haben die Sinusfunktion bereits kennengelernt und den Zusammenhang zwischen dem Einheitskreis und der Sinusfunktion erfasst. Darüber hinaus haben sie bereits Erfahrungen mit dem Einfluss von Parametern auf Potenzfunktionen und die Exponentialfunktionen gesammelt. Sie verfügen bereits über Grundlagenwissen im Umgang mit dem GeoGebra-Suite Applet.
Bildungsplanbezug
Im Bildungsplan steht in den inhaltsbezogenen Kompetenzen für die Klassenstufen 9/10, dass die Schülerinnen und Schüler neue Funktionstypen (wie die Sinusfunktion) kennenlernen und an dieser Stelle ihr "[...] Wissen über die Wirkung von Parametern auf Graphen [vertiefen]" (Bildungsplan, 2016, S.34). In Bezug auf die trigonometrischen Funktionen fordert er konkret, dass die Schülerinnen und Schüler "[...] die Graphen trigonometrischer Funktionen mit unter Verwendung charakteristischer Eigenschaften skizzieren und die Wirkung der Parameter abbildungsgeometrisch als Streckung, Spiegelung, Verschiebung deuten, auch .
Lernziele
Die Schülerinnen und Schüler sollten nach Bearbeiten der Aufgaben in der Lage sein den Einfluss der Parameter der Sinusfunktion als Streckung, Spiegelung und Verschiebung zu deuten. Darüber hinaus soll ihnen die Arbeit mit GeoGebra dabei helfen den Einfluss der Parameter auf den Funktionsterm und den Funktionsgraphen besser zu verstehen, da die Schüler mit GeoGebra eine "Echtzeit-Manipulation" durchführen können.
Unterrichtsablauf
In der Einheit lernen Schülerinnen und Schüler den Einfluss von Parametern auf die Sinusfunktion kennen. Hierbei werden nicht sofort alle Parameter gleichzeitig sondern nacheinander eingeführt. Mit Hilfe der Schieberegler-Funktion können die Schülerinnen und Schüler direkt mitverfolgen, wie sich eine Veränderung der Parameter auf das Verhalten des Funktionsgraphen auswirkt. Zur Ergebnissicherung müssen sie anschließend einige Fragen beantworten, mit denen das Verständnis für den Einfluss der Parameter konkretisiert werden soll (bspw. Stauchung, Streckung, Spiegelung).
Aufgabe 1.1
a) Gib in das Eingabefeld ein. Der Graph von f(x) wird automatisch in der Grafik-Ansicht angezeigt.
Anmerkung: Stell sicher, dass die Objektname anzeigen Option auf Alle neuen Objekte eingestellt ist, damit du die Namen der Objekte in der Grafik-Ansicht siehst. Du kannst diese in den Einstellungen ändern, indem du rechts auf Global gehst.
b) Gib den Buchstaben a in das Eingabefeld ein und bestätige mit der Eingabetaste. Es wird automatisch ein Schieberegler für a erstellt.
c) Gib die Funktion ein, indem du die Bildschirmtastatur verwendest.
d) Blende nun die Beschriftung der beiden Graphen ein indem du mit einem Rechtsklick auf den jeweiligen Graphen klickst. Dort öffnest du nun mit einem Klick auf die drei übereinander angeordneten Punkte ein Dropdown-Menü in dem du die Einstellungen auswählst. Dort findest du unter dem Reiter Grundeinstellungen ein Kästchen neben dem Beschriftung anzeigen steht. In dem Feld daneben muss Beschriftung & Wert stehen. Ist dies nicht der Fall, dann ändere die Einstellung entsprechend. Anschließend schließt du das Fenster wieder.
e) Bewege den Schieberegler und beobachte, wie sich der Graph der Sinusfunktion verändert.
Gut zu wissen: den Parameter bezeichnet man auch als Amplitude.
Welche Arten der Veränderung am Graphen kannst du beobachten, wenn du den Parameter a änderst?
Wie verhält sich der Graph von g(x) im Vergleich zu dem Graphen von f(x), wenn a > 1 ist? Er ist ...
Wie verhält sich der Graph von g(x) im Vergleich zu dem Graphen von f(x), wenn 0 < a < 1 ist? Er ist ...
Wie verhält sich der Graph von g(x) im Vergleich zu dem Graphen von f(x), wenn -1 < a < 0 ist? Er ist ...
Wie verhält sich der Graph von g(x) im Vergleich zu dem Graphen von f(x), wenn a < 0 ist? Er ist ...
Aufgabe 1.2
a) Gib in das Eingabefeld ein.
b) Wechsle auf der Bildschirmtastatur in die Tastatur, wähle den griechischen Buchstaben aus und drücke die Eingabetaste. Es wird automatisch ein Schieberegler für erstellt.
c) Wiederhole den vorherigen Schritt und erstelle einen Schieberegler für den griechischen Buchstaben .
d) Gib die Funktion ein, indem du die Bildschirmtastatur verwendest.
e) Lass dir wieder die Beschriftungen beider Graphen anzeigen, wie du es in 1.1 d) getan hast.
f) Bewege erst den Schieberegler und anschließend den für und beobachte, wie sich der Graph von g(x) in Bezug auf f(x) ändert, wenn sich die Parameter ändern.
Gut zu wissen: den Parameter nennt man auch Periode, während der Parameter als Phase bezeichnet wird.
Welche Arten der Veränderung am Graphen von g(x) kannst du beobachten, wenn du den Parameter änderst?
In welche Richtung wird der Graph von g(x) verschoben, wenn man positive Werte für einsetzt?
In welche Richtung wird der Graph von g(x) verschoben, wenn man negative Werte für einsetzt?
Welche Arten der Veränderung am Graphen kannst du beobachten, wenn du den Parameter änderst?
Für welche Werte wird der Graph von g(x) im Vergleich zu dem von f(x) gestaucht?
Für welche Werte wird der Graph von g(x) im Vergleich zu dem von f(x) gestreckt?
Aufgabe 1.3
a) Gib in das Eingabefeld ein.
b) Gib den Buchstaben d in das Eingabefeld ein und bestätige mit der Eingabetaste.
d) Gib die Funktion ein, indem du die Bildschirmtastatur verwendest.
c) Lass dir wieder die Beschriftungen beider Graphen anzeigen.
e) Bewege den Schieberegler d und beobachte, wie sich der Graph von g(x) in Bezug auf f(x) ändert, wenn sich der Parameter ändert.
Welchen Einfluss hat der Parameter auf den Graph von g(x) im Vergleich zu dem von f(x)?
Aufgabe 1.4
a) Gib in das Eingabefeld ein.
b) Erstelle einen Schieberegler für den griechischen Buchstaben .
c) Gib die Funktion ein, indem du die Bildschirmtastatur verwendest.
d) Lass dir wieder die Beschriftung beider Graphen anzeigen.
e) Bewege den Schieberegler und beobachte, wie sich der Graph von g(x) in Bezug auf f(x) ändert, wenn sich der Parameter ändert.
Wie du vielleicht festgestellt hast, kommt es immer wieder vor, dass beide Graphen genau übereinander liegen. Das passiert bspw. genau dann, wenn du für einsetzt. Du weißt bereits, dass die Sinusfunktion -periodisch ist. Gib weitere Werte für an, für die gilt
Quellen
Thurm, D. (2019): Digitale Mathematikwerkzeuge im Mathematikunterricht integrieren. Wiesbaden: Springer.
Ministerium für Kultus, Jugend und Sport Baden-Württemberg (2016): Bildungsplan des Gymnasiums - Mathematik. Stuttgart: Neckar-Verlag GmbH.
Sekretariat der Kultusministerkonferenz. (2012). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife. Zugriff am 1.10.2022 unter https://www.kmk.org/fileadmin/veroeffentlichungen_beschluesse/2012/2012_10_18-Bildungsstandards-Mathe-Abi.pdf