"Cicloide" com raio variável

Autor:
Eduardo Toffolo
Tópico:
Área, Cálculo, Expoente, Funções Exponenciais, Funções, Geometria, Inteiros, Cálculo Integral, Curvas paramétricas, Razões, Rotação, Transformação de semelhança ou semelhança, Simetria, Trigonometria
A cicloide é o lugar geométrico de um ponto sobre uma circunferência (com raio constante) que rola sobre uma linha reta. Mas e se nós variarmos o seu raio durante o percurso? Este applet permite visualizar o traço formado ao variar o raio de acordo com o ângulo (em radianos) de rotação da circunferência. Valores negativos para o raio são entendidos como uma circunferência abaixo do eixo x rotacionando para a esquerda (experimente!).
Um resultado bacana é que a área abaixo de um período da cicloide é exatamente 3 vezes a área do círculo que a gerou. Quando variamos o raio, por outro lado, não faz sentido pensar na "área abaixo de um período" pois nem sempre (quase nunca, na verdade) o traço é periódico. Isso nos leva a seguinte pergunta: para quais funções o traço é tal que podemos dividi-lo em intervalos semelhantes (não necessariamente iguais) entre si? Para facilitar o trabalho, colocaremos mais duas restrições: (1) traços de intervalos consecutivos são proporcionais por um fator constante - isso permite calcular a área de qualquer intervalo sabendo a área do primeiro; (2) pontos correspondentes em intervalos distintos estão associados a um mesmo ângulo em relação o eixo vertical (figura 1).

Figura 1

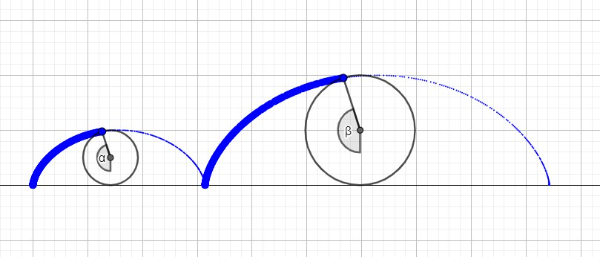
Figura 1
Ângulos iguais em relação ao eixo vertical implica que os ângulos de rotação distam por um múltiplo de 2, isto é, são congruentes módulo 2.

Figura 2

Figura 2
Como é possível notar, a segunda restrição não necessariamente é sempre verdade: é possível que pontos correspondentes em intervalos distintos sejam formados por ângulos não congruentes módulo 2.
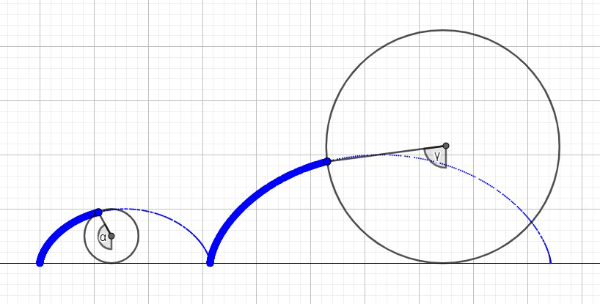
Com as duas restrições, sabemos que o raio em dois pontos correspondentes de intervalos consecutivos são proporcionais pela mesma razão , ou seja, . Algumas soluções para essa equação são: (1) para uma constante. Neste caso, e o traço gerado é a cicloide; (2) e, neste caso, ; (3) ou qualquer combinação de senoides. Neste caso, ; (4) ou qualquer combinação de senoides. Neste caso, . Como se pode perceber, o caso corresponde as funções periódicas e há uma infinidade de outras soluções além das apresentadas. Obs: (1) a solução (3) gera um traço bem conhecido; (2) a solução (4) não repete periodicamente neste applet porque o Geogebra parece não conseguir calcular o valor certo da integral do módulo do seno para pontos fora do intervalo . Consertando isso (manualmente), o resultado é o mostrado na figura 3.

Figura 3

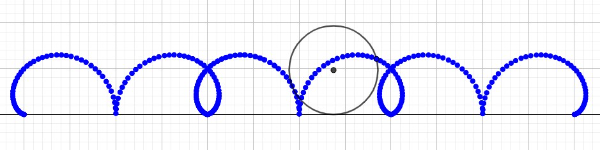
Figura 3
Traço gerado pela solução (4). Compare esse resultado com o cardioide (solução (3)).
Por último, para quem se interessar na construção deste applet, note que as coordenadas do centro da circunferência em função do ângulo de rotação são (de fato, o produto entre o ângulo em radianos e raio da circunferência resulta no arco percorrido para um raio constante: generalizando, temos que a integral do raio em relação ao ângulo resulta justamente no deslocamento horizontal do centro da circunferência). Além disso, as coordenadas do ponto rastreado sobre a circunferência são dadas por (o último termo é o versor que dá a direção do ponto em relação ao centro da circunferência).

Novos Materiais

Descobrir recursos

Explorar Tópicos