5-voudig systeem
succesvol
Uit het vuistdikke boek Islamic Geometric Patterns van Jay Bonner, leer je al snel dat het 5-voudig veelhoekig systeem, dat Lu en Steinhardt beschrijven lang niet het enige veelhoekige systeem was dat als onderliggend patroon gebruikt werd bij het ontwerpen van geometrische patronen, maar wel het meest succesvolle.
Op het eerste zicht verwacht je niet veel heil van een systeem met 5-voudige symmetrieën, omdat je enkel met regelmatige 5-hoeken geen betegelingen kunt maken. Maar het plaatje verandert helemaal wanneer je een systeem hanteert met meerdere tegels.
Het aantal mogelijkheden is eindeloos, maar vanuit een regelmatige 10-hoek kan je een beperkt aantal tegels afleiden die een heel homogeen syteem vormen. Je kunt heel diverse betegelingen creëren zonder andere bijkomende tegels te moeten gebruiken.
vormen afgeleid uit de 10-hoek
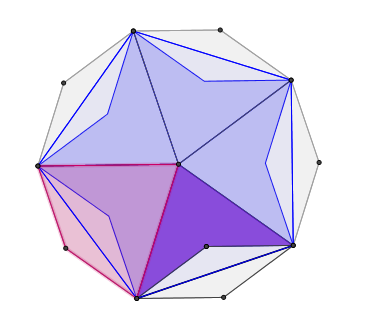
De vijfhoek, de ton, de lange zeshoek en de strik zijn geen toevallige vormen. Je kunt ze gemakkelijk construeren door binnen een regelmatige 10-hoek enkele lijnen te trekken.
combineren
De gebruikte vormen binnen het 5-voudig systeem laten zich vlot combineren en volgen zelfs op een logische manier uit het gebruik van de 10-hoek in een betegeling.
- Schik je 10-hoeken zo dicht mogelijk tegen elkaar, dan vullen strikken de overblijvende ruimte op.
- Omring je 10-hoeken door een ring van 5-hoeken, dan volgt de ton (als overlapping van twee 5-hoeken) als het sluitstuk van twee ringen.
overlapping
De lange zeshoek en de ton kan je ook definiëren vanuit overlappingen.
- Twee deels overlappende 10-hoeken bepalen de lange 6-hoek
- Twee deels overlappende 5-hoeken bepalen de ton.
flexibiliteit
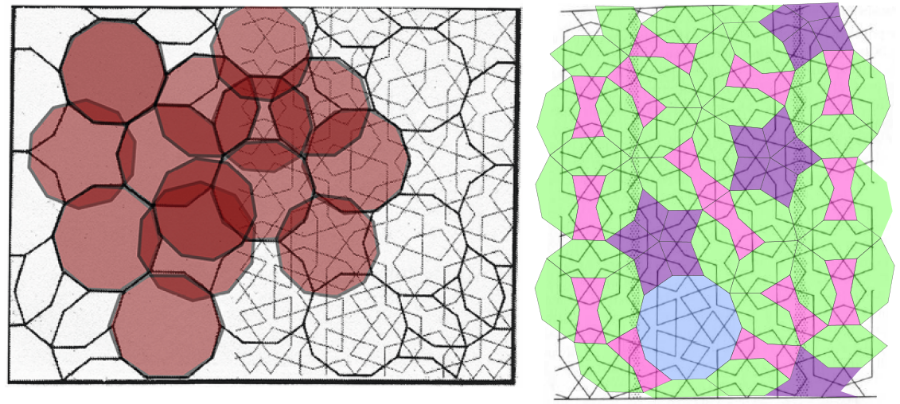
De ontwerpers van Islamitische geometrische patronen ontwikkelden al heel snel een sterk inzicht in de mogelijkheden om de eigenschappen van devormen van het 5-voudig systeem om te zetten in een verbluffende variëteit en complexiteit van patronen. De wandpanelen van de Gunbad-i Kabud illustreren het gebruik van overlappende 10-hoeken en de alternatieve opvulling van een 10-hoek door drie lange zeshoeken en een strik om af te wijken van de meest eenvoudige regelmatige oplossingen en lokale gebieden met 5-hoekige symmetrie te crceëren(= paarse sterren).
Penrose
Een wiskundige die na 1974 zulk patroon bekijkt, legt al snel verbanden met Penrose.
Je ziet onmiddellijk de paarse stervormen, omgeven door wat lijkt op de Penrose karrewielen en lokale patronen waarbinnen de symmetrie doorbroken wordt door een alternatieve opvulling. En natuurlijk is er de afleiding van vlieger en pijl binnen een 10-hoek zelf, die je herkent in de sterfiguren van Maragha, die gevormd worden door overlappende 10-hoeken.