Semelhança de triângulos
Quando se trata de triângulos, a semelhança ocorre quando os três ângulos são ordenadamente congruentes e as medidas dos lados homólogos (mesma posição) são proporcionais.
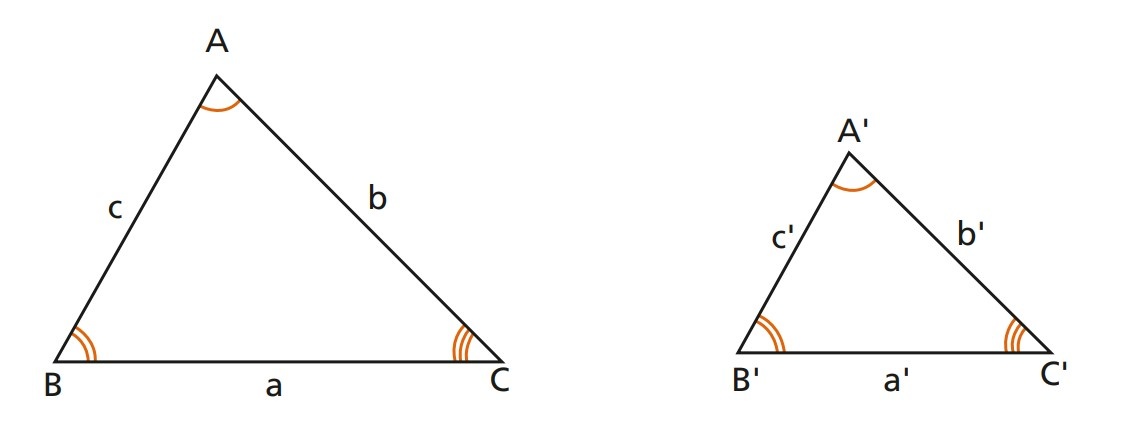
Nos triângulos ABC e A'B'C':
- Os ângulos correspondentes são congruentes: e ;
- Os ângulos homólogos são proporcionais: .
Casos de semelhança
1º - Ângulo, Ângulo (AA): quando dois ângulos são ordenadamente congruentes.
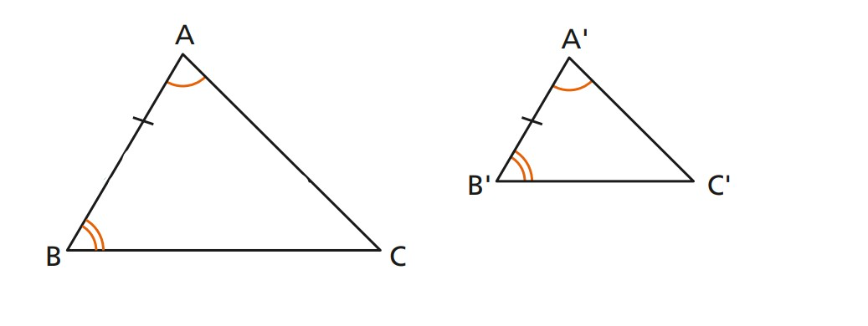
2º - Lado, Lado e Lado (LLL): quando os lados homólogos são proporcionais.
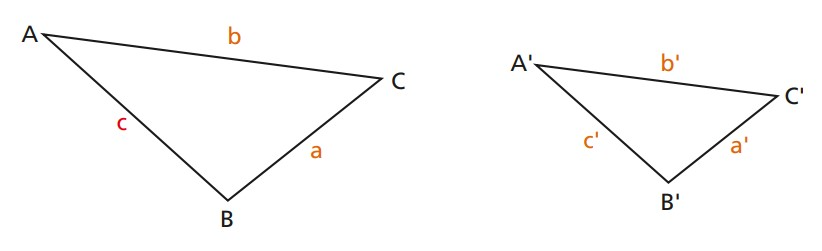
3º - Lado, Ângulo e Lado (LAL): quando possuem dois lados homólogos proporcionais e o ângulo compreendido entre eles é congruente.
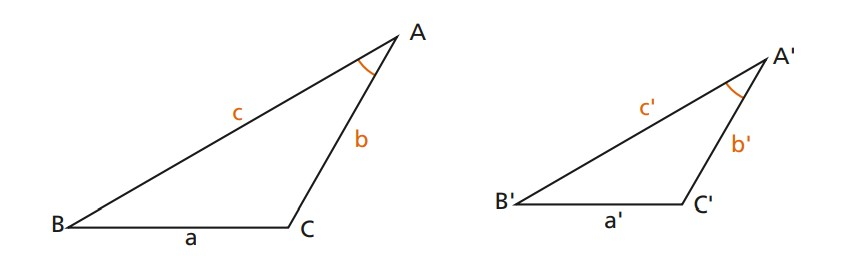
Com base nos critérios de semelhança de triângulos, temos que, se a razão de semelhança é k:
a razão entre os perímetros é k;
a razão entre as alturas é k;
a razão entre as áreas é k.