EQUAÇÃO GERAL DA RETA DADO DOIS PONTOS
A equação geral da reta é uma das maneiras de descrever a reta de forma algébrica por meio de uma equação. Na geometria analítica, os objetos geométricos são estudados extensivamente, representados no plano cartesiano, e a partir dessa análise é que se busca descrever os objetos geométricos de forma algébrica. Então, a equação geral da reta é uma relação entre uma equação algébrica e a representação geométrica dessa equação, que é uma reta.
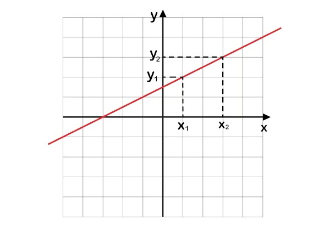
A equação geral de uma reta é igual a ax + by + c = 0, em que a, b e c são coeficientes reais e a e b são diferentes de zero. Para encontrar a equação geral de uma reta, é necessário conhecer pelo menos dois pontos dessa equação. Após descobrir esses dois pontos, aplicam-se alguns métodos para encontrar a equação da reta que passa por ambos.
Método 1 para encontrar a equação geral da reta
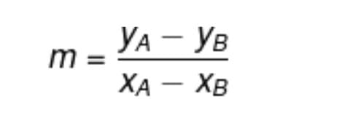
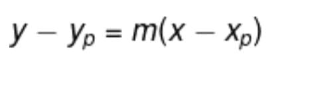
Utilizando o método 1, qual a equação da reta que passa pelos pontos A(2,1) e B(4,7)?
Utilizando o método 2 encontre a equação da reta que passe pelos pontos C(3,3) e D(-1,1).
Dada a equação da reta 2x + y -4 = 0, identifique dois pontos que pertence a essa reta.
REPRESENTAÇÃO GRÁFICA
No campo de entrada digite as equações da reta encontradas e dadas nas questões anteriores. Anote o que você observou.