Aplicação do Teorema de Rolle
Teorema de Rolle
Seja f : [a,b] R contínua, derivável em ]a,b[, tal que f(a) = f(b). Então existe c ]a,b[, tal que f’(c) = 0.
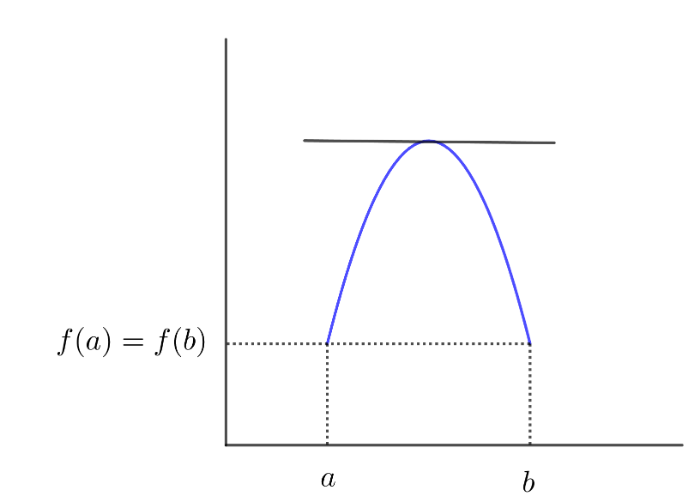
Exemplo de Aplicação do Teorema de Rolle.
01) Verifique se as hipóteses do teorema de Rolle são satisfeitas para a função da abaixo no intervalo (a, b).
f(x) = -x²+ 4x (0,4)
Solução:
1ª hipótese: A função f tem que ser contínua, como a função polinomial é contínua, logo a primeira
hipótese e satisfeita.
2ª hipótese: f(a) = f (b)
Como pelo nosso intervalo a = 0 e b =4, então calculamos f (a) e f (b):
f(0) = -0²+4.0=0 e seguida calculamos f(4)=-4² - 4.4 = -16 +16 = 0, observamos que f(a) = f(b) = 0
3ª hipótese: f’(c) = 0
f^'(x)=(-2x)^(2-1)+4.1=-2x+4, fazendo f’ (c) = - 2c +4, como f’(c) = 0
-2c+4=0
2c = -4
c==2
Usando o geogebra, poderemos observar essa aplicação graficamente, fazendo os seguintes passos:
1º passo: Abra
o aplicativo geogebra e no campo entrada escreva:
Se (0≤x≤4), -x^2+4x
2° passo:
Observe no gráfico o valor de f(a) e f(b) e o ponto onde f '(c) = 0 movendo o controle deslizante.
3° passo:
Resolva os exercícios a seguir usando o geogebra e faça as observações do passo 2 para cada função.
Exercícios:
a) f(x) = 4x³ - 9x →[-3/2,3/2]
b) f(x) = sen (x)→(0,2π)