TRİGONOMETRİ
Birçok alanda duyduğumuz trigonometri; matematik ve geometrinin en önemli konularından biridir. Nitekim uzaklık ve yükseklik hesaplamalarında, astronomik ölçümlerde, uydu sistemlerinde, fizikte dalgalarda (ses dalgaları, elektromanyetik dalgalar vs.), havacılıkta, navigasyon teknolojilerinde, deniz biyolojisi ve okyanus biliminde, ve tabii ki de kalkülüste trigonometri kullanılmaktadır. Başka bir deyişle, üçgenler ve hatta üçgenlerle en az alakası olan neredeyse her konuda trigonometri var!
Bunlar dışında konuyu daha iyi kavramanız ve sizi düşünmeye itmesi için birçok yere soru yerleştirilmiştir. Bu soruların cevaplarını doğrudan yazmanıza gerek yoktur (sonuçta açık uçlu sorulardır) ancak seyahatinizin daha iyi geçmesi için mutlaka sorular üzerine düşünmeniz ve kontrol cevaplarını okumanız önerilmektedir.
Trigonometri nedir
Birçok alanda duyduğumuz trigonometri; matematik ve geometrinin en önemli konularından biridir. Nitekim uzaklık ve yükseklik hesaplamalarında, astronomik ölçümlerde, uydu sistemlerinde, fizikte dalgalarda (ses dalgaları, elektromanyetik dalgalar vs.), havacılıkta, navigasyon teknolojilerinde, deniz biyolojisi ve okyanus biliminde, ve tabii ki de kalkülüste trigonometri kullanılmaktadır. Başka bir deyişle, üçgenler ve hatta üçgenleri akla getirmeyen konularda dahi trigonometri var!
Bu küçük dijital kitapçıkta bölümler üzerinde yapacağımız seyahat ile trigonometri hakkında fikir sahibi olmakla kalmayıp bu soyut konunun görece somut çıkarımları yapmakta nasıl kullanılabileceğini de göreceğiz.
Öncelikle, trigonometri nedir? Trigonometri, üçgenin kenarları ve açıları arasındaki ilişkileri çalışan, matematiğin bir dalıdır. Peki, bu ilişkiler nasıl ifade edilir ve ne işe yarar?
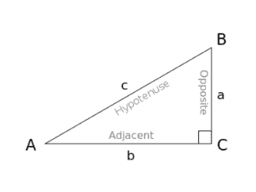
Trigonometrik Fonksiyonlar: Sinüs, kosinüs ve tanjant
Sinüs, o açının karşısındaki kenarın hipotenüse oranıdır.
Kosinüs, o açının komşu kenarının hipotenüse oranıdır. Burada komşu kenar için iki seçenek var gibi gözükse de biri hipotenüs olduğu için komşu kenarla kastedilmek istenenin dik açı ile o açının arasındaki kenar olduğu açıktır.
Tanjant, o açının karşısındaki kenarın komşu kenara oranıdır.
Kotanjant, ise tanjantın tersidir, yani açının komşu kenarının karşı dik kenara oranıdır.
Soru1:
A noktasını hareket ettirdiğinizde ne gözlemlediniz?
Soru2:
Eğimli bir yolda olduğunuzu varsayın. Yolun uzunluğunu ve yüksekliğini bilmiyorsunuz ancak sadece yolun eğiminin başladığı noktanın düz zemin ile yaptığı açıyı biliyorsunuz. Buna göre aşağıdakilerden hangisi size yolun eğimini verir?
Trigonometrik Alıştırmalar ve Problemler
30°, 40°, 50° ve 60° açılarının hem sinüs hem de kosinüs değerlerini hesap makinesi yardımıyla bulunuz. Bir şey fark ettiniz mi? Nedir? Bunun muhtemel açıklamasını düşününüz.
Belirli bir saatte yarım metrelik bir sopanın uzunluğunun gölgesinin uzunluğuna oranı ile bir ağacın uzunluğunun gölgesininkine oranı arasında nasıl bir ilişki vardır? Bunun sebebi ne olabilir? Açıklayınız.
yerde dik duran bir sopanın uzunluğunun, sopanın ucu ile gölgesinin ucu araındaki mesafeye oranını bulmak istiyor. Bu işlemi yapmasının kısa bir yolu var mıdır? Nedir?
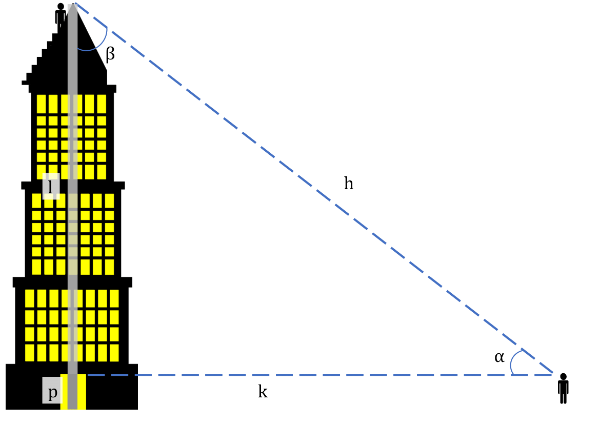
Yukarıdaki şekilde binanın uzunluğunu öğrenmek isteyen birinin aşağıdakilerden hangisini/hangilerini bilmesi yeterlidir? (Her bir şıkkı ayrı düşünün. Birden fazla seçim yapabilirsiniz.)
TRİGONOMETRİ VE BİRİM ÇEMBER
Yukarıdaki şekil yarıçapının 1 birim olması sebebiyle "birim çember" olarak anılır. Dolayısıyla oluşacak üçgenin hipotenüsü sabit olduğu için trigonometrik oranlar kolaylıkla gözlenir. Siz de deneyin!
Ve başka büyük bir faydası da şimdiye kadar uğraştığımız dar açılardan büyük açıların da trigonometrik değerlerini bulabilmemizi sağlar (merkez açıya dikkat edin). Örneğin 120°lik açının sinüsü kaçtır? Bulmak için sürgüyü ya da giriş kutusunu kullanarak C noktasını çemberin sol üst bölgesindeki (koordinat sisteminin II. bölgesindeki) ilk noktaya getirin, burası 120°dir, her bölgedeki rehber noktalar sabit örüntüyle not edilmiştir.
Birim çemberde üçgenin açısı 0°, 180° ve 360° iken kotanjantın değerini kontrol edin. Neden soru işareti çıkıyor? Kotanjantın bu açılar için işlem yapamamasının nedeni nedir?
Her değerin pozitif olduğu bir bölge varken her değerin negatif olduğu bir bölge neden yoktur?
YARATIM/İMGELEME
Bir kağıt ve kalem alın.
Sürgüyü ilerletirken y'nin değerlerini kontrol ediniz (bunun için sinüs değerini veya mavi kenarın uzunluğunu kullanabilirsiniz çünkü hipotenüs halihazırda birimdir ve hem mavi kenar hem de kosinüs apsis değerini verecektir). Ve şu adimları takip edin.
1) Kağıda koordinat sistemini çizin. Apsis, zaman (t) olsun ve ordinat ise yukarıdaki birim çemberdeki y'nin değerlerini (y) göstersin. --> Ancak birim çemberde gözüken değerin 10 katını almanız işlemimiz bittiğinde daha net bir sonuç ortaya çıkaracaktır.
2) Bundan sonra ordinat eksenine birim çemberdeki y'nin alabildiği tüm değerleri yazınız (sinüsün alabildiği tüm değerleri görmek için sürgüyü hareket ettirip sinüsün tüm değişimini gözleyin). Tabii bunu yaparken 10 ile çarpmayı unutmayın.
3) Daha sonra birim çemberde y'nin değişimini yeni koordinat sistemimize taşıyacağız. Nasıl? Açı 0°den 360°'ye değişirken y'nin değişimlerini koordinat sistemine taşıyın ama bunu yaparken 15°lik değişimi zaman yerine koyun.
4) 3. adımı merkezi açı 360°'ye ulaşana değin devam ettirin. Bütün noktaları yerleştirdikten sonra noktaları birleştirin ancak genel görünümü dikkate alarak eğrisel bir birleştirme yapmak isteyebilirsiniz. Çiziminiz bittiğinde ilginç bir şekil çıkacaktır. Cevabınızı kontrol etmek için bir sonraki bölüme geçin.
Sinüs Grafiği Nedir
"Birim çember tamam da sinüs grafiği de nedir?" diye soruyor olabilirsiniz. Şöyle ki birim çemberimizdeki üçgenin bir dik kenar uzunluğuna baktığımızda bir şey fark edebiliriz: Bir kenar uzunluğu düzenli bir şekilde artıp azalır. Mesela önceki bölümde görmüş olduğunuz gibi sinüs ile ilgili kenarın uzunluğu önce artar ve 90°de maksimuma ulaşır ve sonra azalıp 180°de 0'a ulaşır. Tabii kenar uzunluğu negatif olamayacağı için burada 180°den sonrası da benzer şekide ilerler: Maks. ile 0 arasında bir nevi salınım görülür.
Bununla birlikte sinüse baktığımızda ise 180°den sonra negatif değerler aldığını görürüz çünkü hatırlayacağınız üzere koordinat sisteminin bölgeleri bu farkı yaratır. Ve işte biz de sinüsün değişimini analiz edip gösterirsek bir sinüs grafiği çıkarabiliriz. Yukarıdaki uygulamada görülen de budur: Birim çemberimiz v sinüs grafiğimiz arasındaki ilişki
(Ancak dikkat ederseniz sinüs grafiğinde sadece ve sadece daha iyi görebilmek uğruna sinüs değerinin 10 katı alınmıştır ki bu sadece dalganın şeklinin t eksenine göre daha belirgin görülmesine olanak tanır.)