Hauptachsentransformation - HAT R²
HAT Ellipse R2
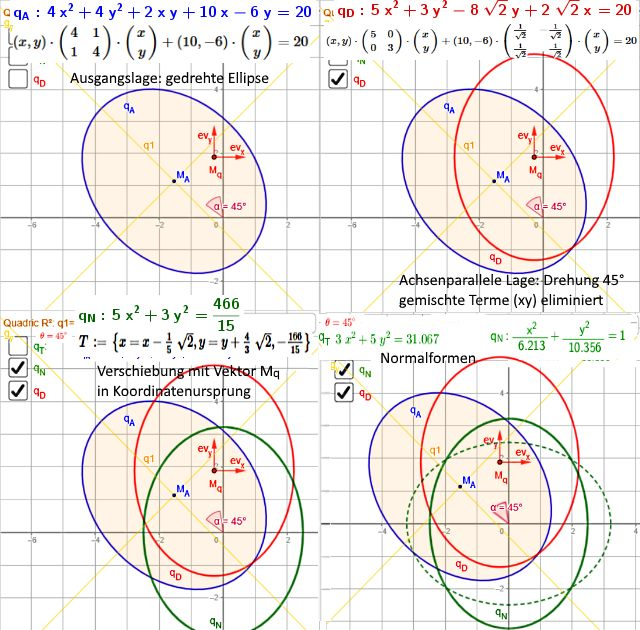
Eine Koordinatentransformation dreht und verschiebt die Koordinatenachsen damit eine Kegelschnittgleichung in Normalform dargestellt werden kann
xT A x + aT x + a0 =0
JordanDiagonalization(A) ==> JD= {Matrix Eigenvektoren JD(1), Diagonalmatrix Eigenwerte JD(2)}
S=JD(1) normalisieren und Determinante =+1 (Drehung erzeugen - ggf. (-1)evi !)
Drehung S (gemischter Summand xy eliminiert)
xT S-1A S x + aTS x + a0 =0 ==> xTD x + aTS x + a0
Quadratische Ergänzung - Translation (Verschiebung)
c11 x2 + c22 y2 = c0
===> Zuordnung des Kegelschnitt zu den Kegelschnitttypen:
Grundlagen: Mathebibel
| Ellipse | {...] | Punkt | |||
| Hyperbel | Geraden X | ||||
| Parabel | Geraden || | oder {..} |
- Ellipse, Punkt oder leere Menge bei gleichem Vorzeichen der Eigenwerte (|A| > 0)
- Hyperbel oder Geradenpaar bei verschiedenem Vorzeichen der Eigenwerte (|A| < 0)
- Parabel, Parallelenpaar, Gerade oder leere Menge, falls 0 ein Eigenwert ist (|A| = 0).
Grundlagen: Mathebibel
HAT Ellipse R² X
Technische Hinweise
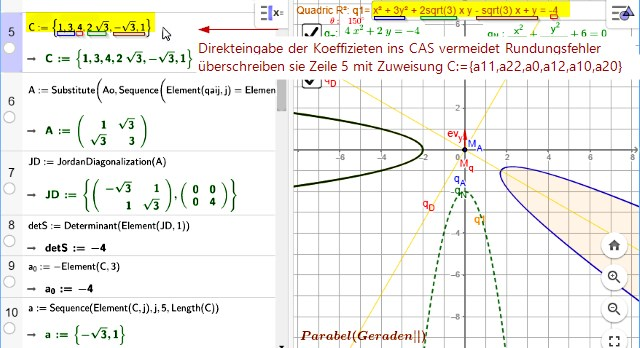
Das Auslesen der Koeffizienten funktioniert z.Z nur über AlgebraView, was zur Rundung von Variablen () führt. Das kann zu Rundungsfehlern, mit z.T. dramatischen Folgen, führen. Z.B.
x² + 3y² + 2sqrt(3) x y - sqrt(3) x + y = -4
==> Arndt Brünners Quadrik-Rechner kommt auf 4x2 = 7943034424934198
In diesen Fällen die Matrixgleichung DIREKT eingeben und die CAS-Zeilen überschreiben.
5: C:={1,3,4,2sqrt(3),-sqrt(3),1}
Nach dem im CAS eingegeben wurde, kann auch die Gleichung auch in die Inputbox geschrieben werden! Falls der Befehl Coeffizents auch im CAS zur Verfügung gestellt wird kann sich das auch mal ändern!
Zum Erstellungszeitpunkt macht es große Probleme das Matrix-Vektor-Produkt einer Quadrikgleichung
xT A x + aT x =ao zu berechnen - einige Workarounds sind eingebaut - falls auf meinen Bugreport reagiert wird kann evtl. darauf verzichtet werden oder schlimmer der Workaround ein Problem werden?
Direkt Eingabe im CAS (zur Vermeidung von Rundungsfehlern)
