Teorema
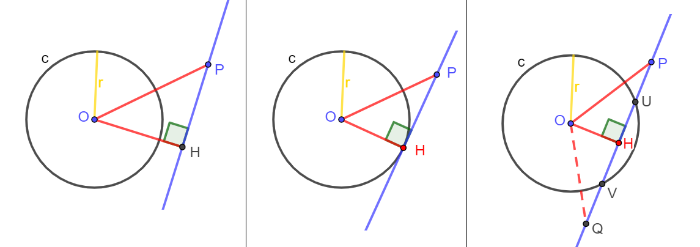
Posizione reciproca tra retta e circonferenza
Date una circonferenza e una retta:
- se la distanza della retta dal centro della circonferenza è maggiore del raggio, la retta è esterna alla circonferenza
- se la distanza della retta dal centro della circonferenza è congruente al raggio, la retta è tangente alla circonferenza
- se la distanza della retta dal centro della circonferenza è minore del raggio, la retta è secante alla circonferenza
Teorema inverso
Se una retta è esterna a una circonferenza, la sua distanza dal centro deve essere maggiore del raggio.
Si dimostra per esclusione.
Infatti, la sua distanza non può essere minore del raggio, altrimenti la retta dovrebbe essere secante; la sua distanza non può essere congruente al raggio, altrimenti la retta dovrebbe essere tangente.
Pertanto, si conclude che la la sua distanza dal centro deve essere maggiore del raggio.
Teorema "riassuntivo"
Data una circonferenza e una retta:
- la retta è esterna alla circonferenza se e solo se la sua distanza dal centro è maggiore del raggio
- la retta è tangente alla circonferenza se e solo se la sua distanza dal centro è congruente al raggio
- la retta è interna alla circonferenza se e solo se la sua distanza dal centro è minore del raggio
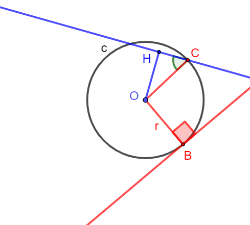
Teorema: La tangente in un punto è perpendicolare al raggio
Se una retta è tangente alla circonferenza, essa è perpendicolare al raggio che ha un estremo nel punto di tangenza.
La retta perpendicolare al raggio nel suo estremo sulla circonferenza è tangente alla circonferenza.
Dimostrazione
La dimostrazione deriva dal teorema riassuntivo, in quanto la distanza di una retta dal centro si riferisce alla perpendicolare. Se la retta è tangente al raggio nel punto di tangenza, la distanza è il raggio e quindi, il raggio è perpendicolare alla tangente.
Se la retta passante per l'estremo di un raggio non fosse perpendicolare, la sua distanza dal centro sarebbe minore del raggio.