Teorema fundamental do cálculo
Para um melhor entendimento do conteúdo proposto, assista ao vídeo introdutório a seguir.
Teorema Fundamental do Cálculo - Vídeo - 01
Introdução ao Teorema Fundamental do Cálculo
O teorema fundamental do cálculo nos permite relacionar as operações de derivação e integração. Ele nos diz que conhecendo a primitiva de uma função contínua , podemos calcular sua integral definida .
Com isso, obtemos de uma maneira rápida e simples de resolver inúmeros problemas práticos que envolvem o cálculo da integral definida.
Tomamos a integral definida , fixamos o limite inferior e fazendo variar o limite superior , então, o valor da integral dependerá desse limite superior variável, que indicaremos por . Fazemos variar no intervalo , obtemos uma função dada por:
Intuitivamente, podemos compreender ambas, através de uma análise geométrica observando a figura a seguir:
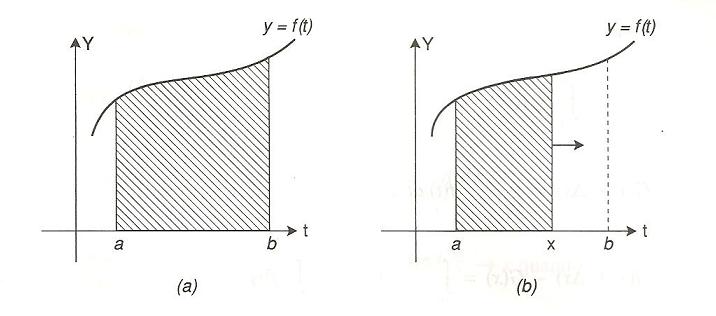
Proposição:
Seja uma função contínua num intervalo fechado . Então a função definida por:
, tem derivada em todos os seus pontos que é dada por:
Uma importante consequência da proposição é que toda função contínua em um intervalo possui uma primitiva que é dada por:
TEOREMA: Se é contínua sobre e se é uma primitiva de nesse intervalo, então
Observamos que a diferença usualmente é denotada por
Renan Lima - Teorema Fundamental do Cálculo - 02
Exemplos Resolvidos Sobre o Teorema Fundamental do Cálculo - 01
Exercícios resolvido Sobre o Teorema Fundamental do Cálculo - 02
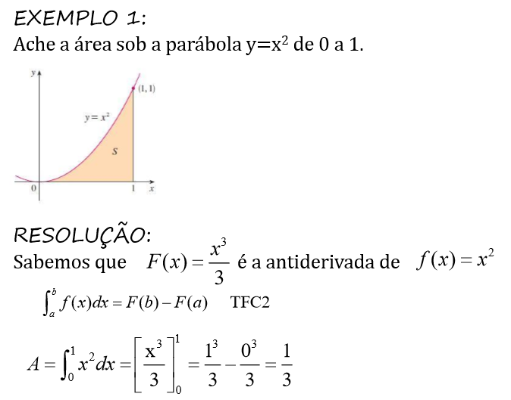
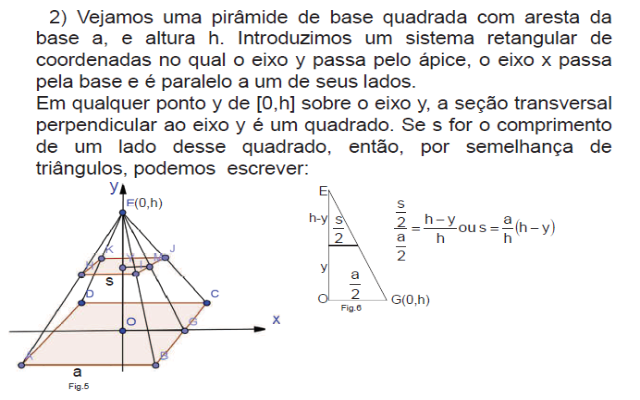

Exercício
Resolva as questões: a)
Utilize a atividade a seguir para verificar o conteúdo estudado.
Você pode utilizar a construção a seguir para verificar as questões do exercício anterior. Para isso, coloque a função da questão no campo destinado a f(x).