Conceptos y Plano Cartesiano

CONTENIDO - Concepto de función - Representación de una función - Función real de variable real - Variable dependiente y variable independiente - Dominio y rango de una función - Raíces o ceros de una función - Sistema de coordenadas rectangulares - Par ordenado y Plano cartesiano CONCEPTO DE FUNCIÓN Si se tienen dos conjuntos A y B, una función f de A en B es una regla que a cada elemento del conjunto A le asigna uno y sólo un elemento del conjunto B. En Fig. 1 se muestra el diagrama sagital o de flechas de tres relaciones.

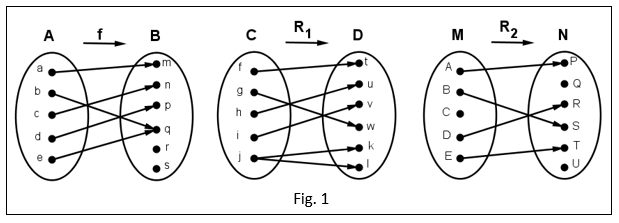
La primera, f de A en B; la segunda, R₁ de C en D y la tercera, R₂ de M en N. - La relación f es función porque todos y cada uno de los cinco elementos del conjunto de partida A, tienen una y sola una imagen en el conjunto de llegada B, a pesar de que hay dos elementos del conjunto B que no son imagen (los elementos r y s). - La relación R₁ No es función porque el elemento j del conjunto de partida C tiene 2 imágenes, k y l, en el conjunto de llegada D. - La relación R₂ No es función porque el elemento C del conjunto de partida M no tiene ninguna imagen en N. Representación de una función En la figura 2 se muestran tres formas diferentes de representar la función f:

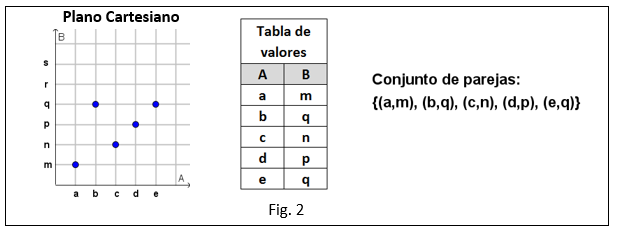
Plano cartesiano: El eje horizontal lo conforman los elementos del conjunto de partida A = {a, b, c, d, e}, y el eje vertical, los elementos del conjunto de llegada B = {m, n, p, q, r, s}. Cada punto representa una pareja de la función: (a,m), (b,q), (c,n), (d,p), (e,q). El primer elemento de la pareja ordenada pertenece al conjunto de partida, A, y el segundo elemento de la pareja pertenece al conjunto de llegada, B. Se dice que m es imagen de a y que a es preimagen de m. Tabla de valores: Es una tabla de doble entrada en la que se registran las parejas de la función. Puede ser horizontal o vertical. En la figura se ha utilizado una tabla vertical: En la primera columna se escriben los elementos del conjunto de partida y en la segunda columna, los elementos del conjunto de llegada. En la primera columna No puede haber elementos repetidos porque cada elemento del conjunto de partida solo puede tener una imagen. En cambio, en la segunda columna Sí pueden haber elementos repetidos como se muestra en la figura: q es imagen de dos elementos, b y e. Conjunto de parejas: Es el conjunto de las parejas ordenadas: {(a, m), (b, q), (c, n), (d, p), (e, f)}. Cada pareja representa un punto en el plano cartesiano. Función real de variable real Función real de variable real es toda regla o correspondencia que a cada elemento de un subconjunto de los números reales, le asigna un elemento del conjunto de los números reales. Normalmente se describe como una expresión matemática o como un enunciado verbal. Ejemplos: 1. - Expresión matemática: f(x) = x + 1,

- Enunciado verbal: A cada número entero se le asigna el entero siguiente. Algunas parejas de f(x) serían: (1, 2), (2, 3), (3, 4), (4, 5), ... 2. - Expresión matemática: g(x) = x² - Enunciado verbal: A cada número real se le asigna su cuadrado. Algunas parejas de g(x) serían: (1, 1), (2, 4), (3,9), ... Variable independiente y variable dependiente Variable independiente de una función es la variable que no depende de otras variables. Normalmente se denota como x. Variable dependiente de una función es la variable que depende de otra variable. Se denota por f(x). En ocasiones se utiliza y = f(x). La variable independiente es x y la variable dependiente es y. En la función f(x) = x + 1, la variable independiente es x. Una vez que se le asigna un valor a x se obtiene un valor único para y. Así por ejemplo, si x = 1 entonces y = 2. Se escribe f(1) = 2. Significa que la imagen de 1 mediante la función f es 2. Esto equivale a la pareja (1, 2). En la función g(x) = x², si x = a, entonces g(a) = a²: la imagen de a mediante la función g es a².

Dominio y Rango de una función Dominio de la función: Es el subconjunto de los números reales en el que se define la función, es decir, el subconjunto de los elementos de los reales que tienen imagen. Se puede denotar como Df. Siguiendo con los dos ejemplos de funciones anteriores, f(x) y g(x) se tiene que: - El dominio de f(x) es el conjunto de los números enteros,

: Todos los números enteros tienen imagen y es única. - El dominio de g(x) es el conjunto de los números reales,

: Todos los números reales tienen imagen y es única. Rango de la función: También se llama recorrido. Es el subconjunto de los reales que son imágenes. Se puede denotar como Rf. - El rango de f(x) es el conjunto de los números enteros,

:Todos los números enteros son imagen de un entero (su anterior). - El rango de g(x) es el conjunto de los números reales mayores o iguales a 0,

: Todos los números reales positivos y el cero son imagen de un real (su raíz cuadrada). Se recuerda que una raíz cuadrada existe en los reales solamente si la cantidad subradical es 0 o es positiva y que tiene dos resultados, uno positivo y uno negativo. Ejemplo,

. Codominio de la función: Es el conjunto de llegada. Para el caso de las funciones reales, el codominio es el conjunto de los reales.

Raíz o ceros de una función Raíces de una función, también llamados ceros, son los valores x en los cuales la función f(x) se hace cero. Si f(a) = 0, entonces una raíz de la función es x = a. La función cruza al eje X en el punto (a, 0). Las raíces pueden ser reales o complejas. Las raíces reales de una función determinan los puntos donde la función cruza o toca al eje X. Si una raíz real se repite, significa que la función es tangente al eje X en ese valor. Sistema de coordenadas rectangulares Sistema de coordenadas rectangulares es también llamado sistema cartesiano en honor del matemático francés Renato Descartes. Cuando el sistema es en dos dimensiones se habla de plano cartesiano. Está formado por dos rectas reales perpendiculares que se cruzan en “cero”. Las rectas perpendiculares se llaman ejes: - el eje horizontal recibe el nombre de eje X o eje de las abscisas. - el eje vertical recibe el nombre de eje Y o eje de las ordenadas. El plano cartesiano se utiliza para ubicar cualquier punto en el plano. Cuando el sistema cartesiano es de tres dimensiones (X, Y, Z), los tres planos son perpendiculares. Se utiliza para representar un punto en el espacio. Par ordenado Par ordenado es una pareja de elementos a y b dados en un determinado orden. Para designar un par ordenado se utiliza la notación (a,b). El primer elemento, a, se llama primera componente y el segundo elemento, b, se llama segunda componente es b. Se hace énfasis en que (a,b) es diferente a (b,a). Coordenadas de un punto en el plano cartesiano: Las coordenadas de un punto corresponde al par ordenado (x,y). La primera componente, x, recibe el nombre de abscisa y es la distancia entre el punto y el eje vertical (eje Y). La segunda componente, y, recibe el nombre de ordenada y es la distancia entre el punto y el eje horizontal (eje X). En la Fig. 3 se muestran en el plano cartesiano, los puntos P, Q, R y S. El valor de la abscisa de cada punto se muestra como el vector (flecha) de color rojo, mientras que el valor de la ordenada se muestra con el vector de color azul:

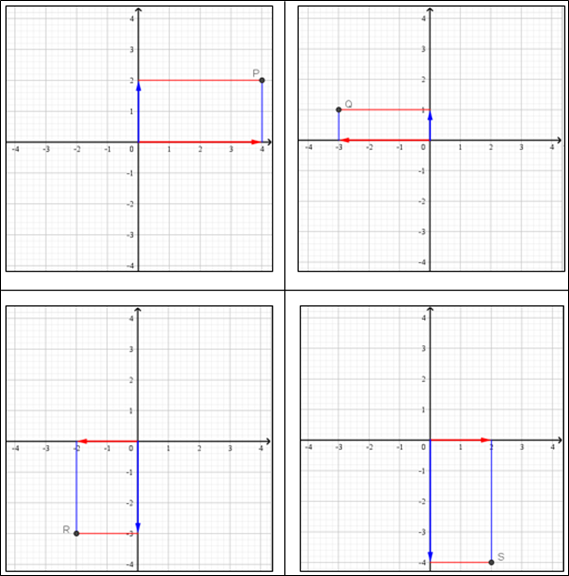
Las coordenadas de cada punto son: P = (4,2) Q =(-3,1) R = (-2,-3) S = (2,-4) El applet siguiente tiene por objetivo reforzar el manejo de coordenadas en el plano cartesiano: - Visualizar los valores de abcisa y de ordenada de P, representadas por vectores, lo que permite identificar el sentido positivo o negativo. - Activar el rastro y desplazar el dial de los deslizadores x y y. El rastro que deja el punto P será una recta horizontal o una recta vertical, dependiendo del deslizador que se utilice: Horizontal cuando se desplaza x y vertical cuando se desplaza y. Ejemplo: Si se deplaza x mientras y = 2, se obtiene la horizontal y = 2. Si se desplaza y mientras x = -1, se obtiene la vertical x = -1. Recuerde que los valores de x y de y también se pueden dar por teclado utilizando las casillas de entrada.

Conceptos y Plano Cartesiano

Nuevos recursos

Descubrir recursos

Descubre temas