Übung: Abstand eines Punktes zu einer Geraden
Aufgabenstellung
Durch die Punkte A und B verläuft die Gerade g.
Der Punkt P befindet sich nicht auf der Geraden.
Bestimmen Sie den Abstand des Punktes P zur Geraden g.
Schritt 1
Definieren Sie im CAS alle drei Punkte und die zugehörigen Ortsvektoren. Notieren Sie die Ortsvektoren auch im Heft.
Lösung für den ersten Schritt
Schritt 2
Jetzt definieren Sie einen Punkt R auf der Geraden durch die Punkte A und B ganz allgemein mit einem Parameter .
Später werden Sie den Parameter so bestimmen, dass der Abstand zwischen dem Punkt R und dem Punkt P minimal ist. Das ist dann der Fall, wenn der Verbindungsvektor zwischen den Punkten R und P senkrecht zur Geraden ist.
Jetzt schreiben Sie im CAS und im Heft erst einmal die Parameterform für den Ortsvektor des Punktes R auf der Geraden g auf.
Lösung für den zweiten Schritt
Schritt 3
Der Differenzvektor \vec{d}=\vec{p}-\vec{r} verbindet die beiden Punkte R und P. Wenn man den Betrag berechnet, dann errechnet man damit den Abstand der Punkte R und P.
Definieren Sie im CAS den Differenzvektor
Lösung Schritt 3
Schritt 4
Der Abstand zwischen den Punkten R und P variiert, je nach dem Wert des Parameters .
Der Abstand zwischen dem Punkt P und der Geraden g ist der kürzeste mögliche Abstand zwischen R und P. Den hat man dann erreicht, wenn der Differenzvektor senkrecht zur Geraden g ist.
Diese Bedingung kann man mithilfe des Skalarproduktes mathematisch formulieren.
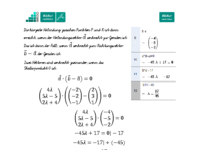
Schreiben Sie die Bedingung auf, dass der Differenzvektor senkrecht zur Geraden g sein soll.
Lösen Sie die entstandene Gleichung nach
Lösung Schritt 4
Schritt 5
Den Wert, den Sie für errechnet haben, setzen Sie nun in den Differenzvektor ein und Sie berechnen den Betrag . Damit haben Sie den Abstand zwischen der Geraden und dem Punkt P berechnet.