graphisches Lösen

Wichtig: Hinweis

Wenn du im Unterricht die "linearen Funktionen" und "Geraden" noch nicht behandelt hast, kannst du dieses Kapitel unmöglich verstehen. Mache in diesem Fall mit dem Kapitel "algebraische Lösungsverfahren" oder "Lösen durch (systematisches) Raten" weiter! Wenn du beide Kapitel bereits bearbeitet hast, kannst du mit "Die Lösung des Problems" weitermachen.

Beispiel

Stell dir vor, du sollst folgendes Gleichungssystem lösen:

I y - x = 6 II y + 3x = -2

Diese beiden Gleichungen können wir natürlich jeweils beliebig umstellen (indem wir bei der ersten Gleichung auf beiden Seiten x addieren und bei der zweiten Gleichung auf beiden Seiten 3x abziehen). Dann wird aus dem Gleichungssystem folgendes neues Gleichungssystem:

I y = x + 6 II y = -3x -2

Betrachte die erste Gleichung y=x+6

Diese Gleichung kann man auch interpretieren als:

Wähle alle richtigen Antworten aus

A
Term
B
Funktionsgleichung einer linearen Funktion
C
Funktionsgleichung einer quadratischen Funktion

Antwort überprüfen (3)

Das Selbe gilt natürlich auch für die zweite Gleichung! Wir können uns also statt des Gleichungssystems denken, dass wir zwei Funktionsgleichungen zu zwei Geraden vor uns haben. Wir suchen nun die x- und y-Werte, die eingesetzt in die beiden (Funktions-)Gleichungen eine wahre Aussage erzeugen. Das bedeutet also: Wir suchen einen Punkt (bzw. seine x- und y-Koordinate), der auf beiden Geraden liegt. Oder anders gesagt: Wir suchen den Schnittpunkt! Wir müssen also nur die beiden Geraden, die zu den Gleichungen passen zeichnen und den Schnittpunkt ablesen.

Zeichnung der Graphen in einem Koordinatensystem:

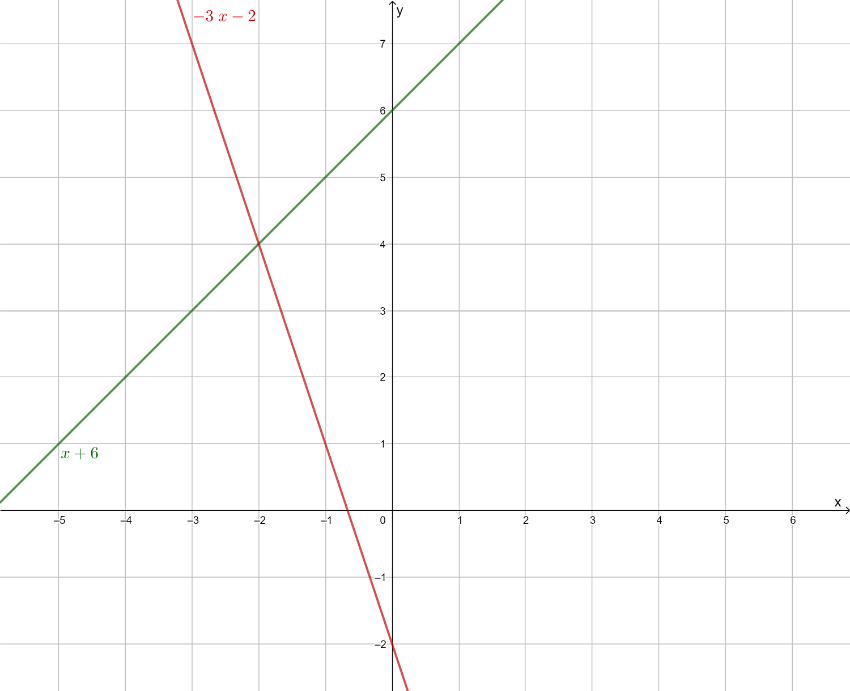
Wir lesen nun also ab: Die Graphen schneiden sich am Punkt (-2 ; 4). Also löst x = -2 und y = 4 unser Gleichungssystem.

Hast du das graphisches Lösen verstanden?

Schreibe in folgendes Eingabefeld eine stichpunktartige Anleitung für das graphische Lösungsverfahren. Vergleiche deine Stichpunktartige Anleitung mit der Musterlösung hier unter "Antworten überprüfen".

Antwort überprüfen

Beschreibe Probleme dieses Verfahrens!

Antwort überprüfen

Fertig?

Mach mit dem Kapitel "algebraische Lösungsverfahren" oder "Lösen durch (systematisches) Raten" weiter, wenn du mit dieser Seite fertig bist und alles verstanden hast. Wenn du beide Kapitel bereits bearbeitet hast, kannst du mit "Die Lösung des Problems" weitermachen.