L2.3 - Congruent Triangles, Part 1
Learning Intentions and Success Criteria
- Justify (orally and in writing) that two triangles are congruent if and only if all corresponding sides and angles are congruent.
- Explain why if all the corresponding sides and angles of two triangles are congruent, then the triangles are congruent.
3.1: True or . . . Sometimes True?: Triangles
∆ABC ≅ ∆A'B'C' If triangle ABC is congruent to triangle A’B’C’. . . 1. What must be true?
2. What could possibly be true?
3. What definitely can’t be true?
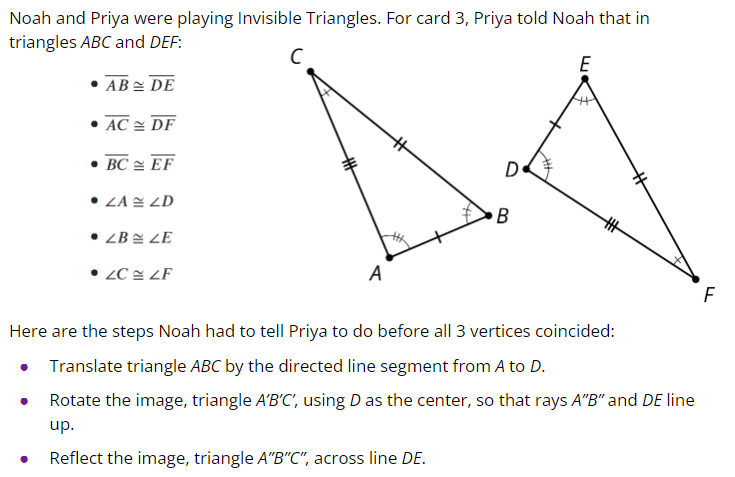
3.2: Invisible Triangles


Transformer Notes
If you are the Player 1 - transformer, write your notes about which parts correspond in the triangles that your partner tells you.
Triangles Notes
If you are the Player 2 - triangles, write your notes about the instructions from your partner - transformer.
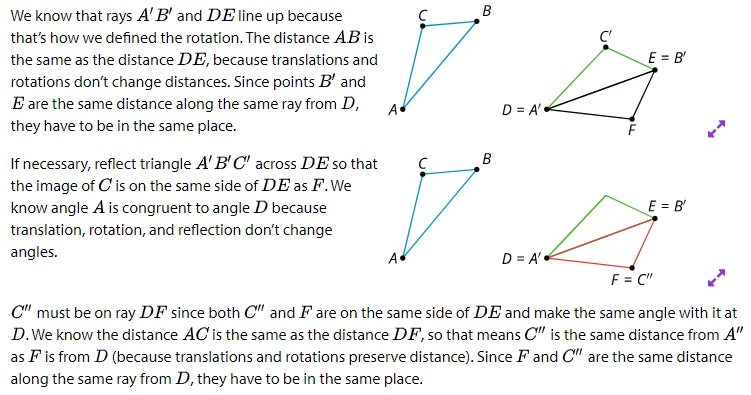
3.3: Why Do They Coincide?

1. We know that rays A”B” and DE line up because we said they had to, but why do points B” and E have to be in the exact same place?
2. Finally, reflect the image, triangle A”B”C” across DE. a. How do we know that now, the image of ray A”C” and ray DF will line up?
b. How do we know that the image of point C” and point F will line up exactly?
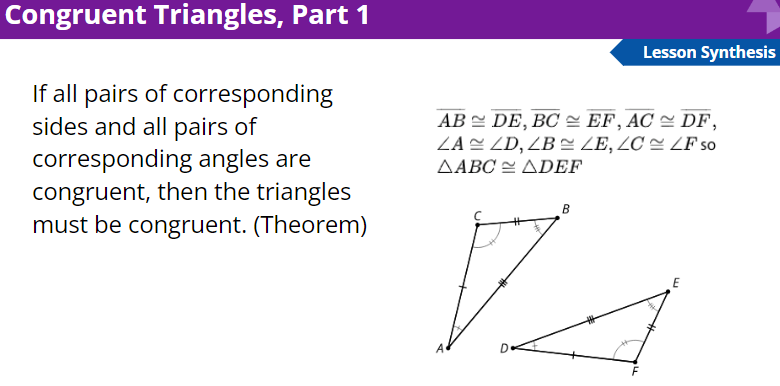


Learning Intentions and Success Criteria
- Justify (orally and in writing) that two triangles are congruent if and only if all corresponding sides and angles are congruent.
- Explain why if all the corresponding sides and angles of two triangles are congruent, then the triangles are congruent.
Cool-Down: Reflecting on Proof
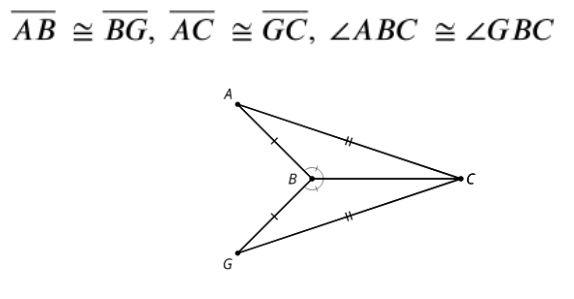
1. What rigid transformation will take triangle GBC onto triangle ABC?
2. Explain why G’ will coincide with A.
3. Is triangle GBC congruent to triangle ABC? Explain your reasoning.
