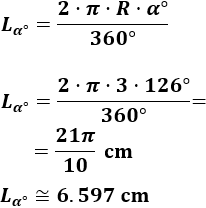Longitud de Arco de Circunferencia
En esta página proporcionamos la fórmula para calcular la longitud de un arco de circunferencia en función de su ángulo y del radio.
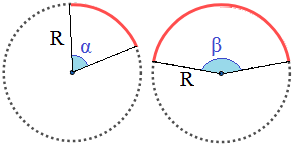
Arco de Circunferencia
Fórmulas
Por el modo en el que hemos definido el arco (porción de una circunferencia), para calcular su longitud sólo tenemos que dividir la longitud de una circunferencia.
La longitud de una circunferencia (o el perímetro de un círculo) es 2⋅π⋅R, siendo R su radio.
Fórmula con el ángulo en grados:
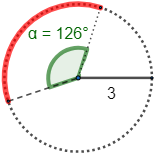
Como una circunferencia es un arco con ángulo de 360 grados, la longitud de un arco con ángulo α en grados es
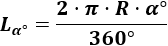 Fórmula con el ángulo en radianes:
Si escribimos el ángulo β en radianes, la fórmula es
Fórmula con el ángulo en radianes:
Si escribimos el ángulo β en radianes, la fórmula es
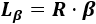
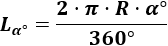 Fórmula con el ángulo en radianes:
Si escribimos el ángulo β en radianes, la fórmula es
Fórmula con el ángulo en radianes:
Si escribimos el ángulo β en radianes, la fórmula es
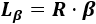
Problemas Propuestos
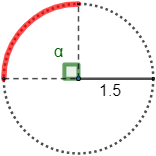
Problema 2
Calcular la longitud del siguiente arco (radio R=1.5 km y ángulo α=π/2 rad):
 Problema 3
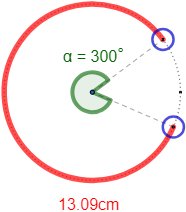
Calcular el diámetro de la muñeca de Ana si su pulsera magnética (que le viene ajustada) mide 13.09 cm:
Problema 3
Calcular el diámetro de la muñeca de Ana si su pulsera magnética (que le viene ajustada) mide 13.09 cm:
 Problema 4
Calcular el perímetro (en azul) de la siguiente figura construida con arcos de circunferencias de radios 1, 2 y 3 metros:
Problema 4
Calcular el perímetro (en azul) de la siguiente figura construida con arcos de circunferencias de radios 1, 2 y 3 metros:
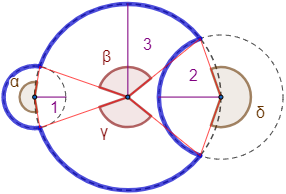 Los ángulos son α=200∘, β=122∘, γ=122∘ y δ=219∘.
Problema 5
Los ángulos son α=200∘, β=122∘, γ=122∘ y δ=219∘.
Problema 5
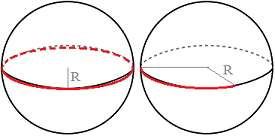 Se tiene una cuerda roja que mide 63π/4 metros (aproximadamente, 49.48 metros) y se utiliza para rodear con una única vuelta una esfera metálica de radio R metros por su ecuador.
Se corta el trozo de cuerda que sobra y se intenta hacer lo mismo con una esfera idéntica, pero sólo hay suficiente para un arco de 5π/8 radianes.
¿Cuánto mide el radio R de las esferas?
Soluciones: Longitud de arco de circunferencia.
Se tiene una cuerda roja que mide 63π/4 metros (aproximadamente, 49.48 metros) y se utiliza para rodear con una única vuelta una esfera metálica de radio R metros por su ecuador.
Se corta el trozo de cuerda que sobra y se intenta hacer lo mismo con una esfera idéntica, pero sólo hay suficiente para un arco de 5π/8 radianes.
¿Cuánto mide el radio R de las esferas?
Soluciones: Longitud de arco de circunferencia.
 Problema 3
Calcular el diámetro de la muñeca de Ana si su pulsera magnética (que le viene ajustada) mide 13.09 cm:
Problema 3
Calcular el diámetro de la muñeca de Ana si su pulsera magnética (que le viene ajustada) mide 13.09 cm:
 Problema 4
Calcular el perímetro (en azul) de la siguiente figura construida con arcos de circunferencias de radios 1, 2 y 3 metros:
Problema 4
Calcular el perímetro (en azul) de la siguiente figura construida con arcos de circunferencias de radios 1, 2 y 3 metros:
 Los ángulos son α=200∘, β=122∘, γ=122∘ y δ=219∘.
Problema 5
Los ángulos son α=200∘, β=122∘, γ=122∘ y δ=219∘.
Problema 5
 Se tiene una cuerda roja que mide 63π/4 metros (aproximadamente, 49.48 metros) y se utiliza para rodear con una única vuelta una esfera metálica de radio R metros por su ecuador.
Se corta el trozo de cuerda que sobra y se intenta hacer lo mismo con una esfera idéntica, pero sólo hay suficiente para un arco de 5π/8 radianes.
¿Cuánto mide el radio R de las esferas?
Soluciones: Longitud de arco de circunferencia.
Se tiene una cuerda roja que mide 63π/4 metros (aproximadamente, 49.48 metros) y se utiliza para rodear con una única vuelta una esfera metálica de radio R metros por su ecuador.
Se corta el trozo de cuerda que sobra y se intenta hacer lo mismo con una esfera idéntica, pero sólo hay suficiente para un arco de 5π/8 radianes.
¿Cuánto mide el radio R de las esferas?
Soluciones: Longitud de arco de circunferencia.Recursos:
- Sectores Circulares
- Coronas Circulares
- Áreas de figuras con formas circulares
- Problemas de Cuadrados
- Problemas de Pentágonos Regulares
- Problemas de Hexágonos Regulares
- Calculadoras de Pentágonos
- Calculadoras de Hexágonos
- Calculadoras de Circunferencias, arcos, sectores y coronas
- Áreas de Triángulos
- Problemas de trigonometría (seno y coseno)
- Teorema de Pitágoras
- Ejercicios interactivos de Geometría 2D
- Matesfacil.com