TEOREMA DE TALES
TRABALHO FEITO POR : MARINA ALVES DOS SANTOS E NICOLAS MATEUS SALVADOR PEREIRA
CONTEXTO HISTÓRICO
O Teorema de Tales, desenvolvido por Tales de Mileto por volta de 650 a.C., estabelece uma relação proporcional entre retas paralelas e transversais. O filósofo grego, reconhecido como o "Pai da Geometria Descritiva" e "Primeiro Matemático", formulou essa propriedade ao observar a sombra de uma pirâmide durante suas viagens, especialmente ao medir a Pirâmide de Quéops no Egito.
Segundo relatos de Hicrônimos, discípulo de Aristóteles, Tales determinou a altura da pirâmide com base no comprimento de sua sombra, especificamente quando a sombra era igual à altura do monumento. Outra versão, narrada por Plutarco, filósofo e historiador grego, descreve que Tales empregou um objeto, possivelmente uma vara, fincada no solo no extremo da sombra projetada pela pirâmide, formando dois triângulos semelhantes.
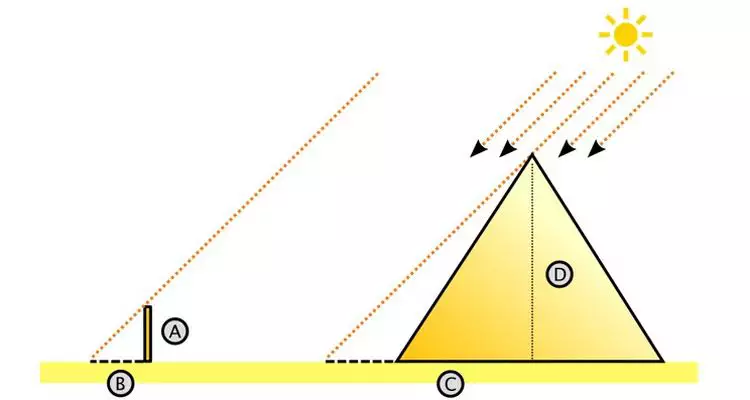
A partir dessa experiência, Tales percebeu que os raios solares incidentes na Terra eram inclinados e paralelos entre si. Essa observação o levou à conclusão de uma relação de proporcionalidade entre as medidas do comprimento da sombra e da altura dos objetos. O enunciado fundamental do Teorema de Tales afirma que, se duas retas são transversais a um conjunto de retas paralelas, então a razão entre dois segmentos quaisquer de uma delas é igual à razão entre os segmentos correspondentes da outra.
DEFINIÇÕES NECESSÁRIAS PARA ENTENDER O TEOREMA
Feixe de retas paralelas Um conjunto de retas coplanares que são paralelas entre si.
Transversal do feixe de retas Uma reta que, pertencendo ao plano de um feixe de retas paralelas, intersecta todas as retas desse feixe.
Pontos correspondentes São aqueles que pertencem a ambas as transversais e estão situados ao longo da mesma reta no feixe.
Segmentos correspondentes São representados por segmentos cujas extremidades coincidem com os pontos correspondentes dessas transversais.
f e g são transversais.
h, i, j, k, l, m, n e p são feixes de retas paralelas.
e , e , e , e são pontos correspondentes.
e , e são segmentos correspondentes.
PROPRIEDADE
Se considerarmos duas retas transversais que cortam um conjunto de retas paralelas distintas e um segmento em uma dessas retas é dividido em p partes congruentes entre si, ao traçar retas a partir dos pontos de divisão para o feixe de retas, podemos concluir que o segmento correspondente na outra reta transversal:
- Também é dividido em p partes;
- E essas partes também são congruentes entre si.