Wie gemalt
Max und Sarah wollen die Farbe in drei gleich große Teilmengen aufteilen - eine für die Vorderseite, eine für die beiden Seitenwände und eine für die Rückseite.
Dafür haben sie eine flache breite Schüssel und einen schmalen hohen Eimer geholt.
5.3 Stellt euch vor, sie würden in jedes Gefäß genau 300 ml gießen. Wie würde sich der Füllstand in der Schüssel und im Eimer unterscheiden? Woran liegt das?
Ach je, das macht das gleichmäßige Aufteilen nicht leichter...
Am besten macht ihr euch wieder ein Bild von dem Zusammenhang - mit einem Graphen.
Hier seht ihr den Graphen, der zu den Werten des Cocktailglases gehört (= Füllgraph).
(Der Graph passt vielleicht nicht ganz genau auf eure Werte, weil man beim Messen und Umschütten immer ein bisschen ungenau ist.)
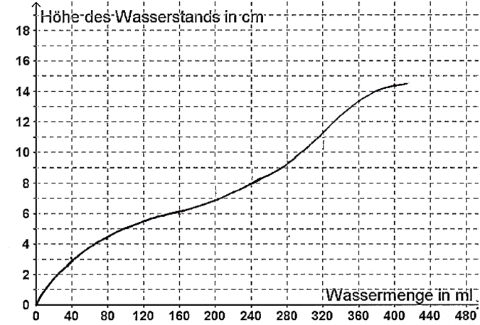
5.4 Erklärt, warum es sinnvoll ist, die Punkte zu verbinden. Denkt daran, was ihr hierzu bei Kreisen und Würfeln gelernt habt!
5.5 Markiert im Füllgraphen des Cocktailglases in eurem Arbeitsheft, wann das Wasser
besonders schnell steigt.
Beschreibt, wie die Geschwindigkeit, mit der das Wasser steigt, mit der Form des Glases zusammenhängt!
5.6 Beschreibt nun mithilfe des Graphen möglichst genau, wie das Wasser im Cocktailglas ansteigt. Verwendet die folgenden Begriffe: langsam, schnell, steil, flach, steigen, breit, schmal