Putting It All Together
Unit 1: Rigid Transformations and CongruenceEstimated Number of Days: 20
Work with transformations of plane figures in Mathematics 8 draws on earlier work with geometry and geometric measurement. Students began to learn about two- and three-dimensional shapes in kindergarten, and continued this work in grades 1 and 2, composing, decomposing, and identifying shapes. Students’ work with geometric measurement began with length and continued with area. Students learned to “structure two-dimensional space,” that is, to see a rectangle with whole-number side lengths as composed of an array of unit squares or composed of iterated rows or iterated columns of unit squares. In grade 3, students distinguished between perimeter and area. They connected rectangle area with multiplication, understanding why (for whole-number side lengths) multiplying the side lengths of a rectangle yields the number of unit squares that tile the rectangle. They used area diagrams to represent instances of the distributive property. In grade 4, students applied area and perimeter formulas for rectangles to solve real-world and mathematical problems, and learned to use protractors. In grade 5, students extended the formula for the area of rectangles to rectangles with fractional side lengths. In Mathematics 6, students combined their knowledge of geometry and geometric measurement to produce formulas for the areas of parallelograms and triangles, using these formulas to find surface areas of polyhedra. In Mathematics 7, students worked with scaled copies and scale drawings, learning that angle measures are preserved in scaled copies, but areas increase or decrease proportionally to the square of the scale factor. Their study of scaled copies was limited to pairs of figures with the same rotation and mirror orientation. Viewed from the perspective of Mathematics 8, a scaled copy is a dilation and translation, not a rotation or reflection, of another figure.In Mathematics 8, students extend their reasoning to plane figures with different rotation and mirror orientations.Through activities designed and sequenced to allow students to make sense of problems and persevere in solving them (MP1), students use and extend their knowledge of geometry and geometric measurement. They begin the unit by looking at pairs of cartoons, each of which illustrates a translation, rotation, or reflection. Students describe in their own words how to move one cartoon figure onto another. As the unit progresses, they solidify their understanding of these transformations, increase the precision of their descriptions (MP6), and begin to use associated terminology, recognizing what determines each type of transformation, e.g., two points determine a translation. They identify and describe translations, rotations, and reflections, and sequences of these. In describing images of figures under rigid transformations on and off square grids and the coordinate plane, students use the terms “corresponding points,” “corresponding sides,” and “image.” Students learn that angles and distances are preserved by any sequence of translations, rotations, and reflections, and that such a sequence is called a “rigid transformation.” They learn the definition of “congruent”: two figures are said to be congruent if there is a rigid transformation that takes one figure to the other. Students experimentally verify the properties of translations, rotations, and reflections, and use these properties to reason about plane figures, understanding informal arguments showing that the alternate interior angles cut by a transversal have the same measure and that the sum of the angles in a triangle is 180º. The latter will be used in a subsequent Mathematics 8 unit on similarity and dilations. Throughout the unit, students discuss their mathematical ideas and respond to the ideas of others (MP3, MP6). Many of the lessons in this unit ask students to work on geometric figures that are not set in a real-world context. This design choice respects the significant intellectual work of reasoning about area. Tasks set in real-world contexts are sometimes contrived and hinder rather than help understanding. Moreover, mathematical contexts are legitimate contexts that are worthy of study. Students do have opportunities in the unit to tackle real-world applications. In the culminating activity of the unit, students examine and create different patterns formed by plane figures. This is an opportunity for them to apply what they have learned in the unit (MP4). In this unit, several lesson plans suggest that each student have access to a geometry toolkit. These contain tracing paper, graph paper, colored pencils, scissors, ruler, protractor, and an index card to use as a straightedge or to mark right angles, giving students opportunities to develop their abilities to select appropriate tools and use them strategically to solve problems (MP5). Note that even students in a digitally enhanced classroom should have access to such tools; apps and simulations should be considered additions to their toolkits, not replacements for physical tools. Enduring Understandings go beyond discrete facts or skills to focus on larger concepts, principles, or processes. They are transferable–applicable to new situations within or beyond the subject. A good essential question is open-ended, thought-provoking, intellectually engaging and calls for higher-order thinking, such as analysis, inference, evaluation, prediction. It cannot be effectively answered by recall alone. For Enduring Understandings, answer, "What specifically do you want students to understand?" For Essential Questions, answer, "What thought-provoking questions will foster inquiry, meaning making, and transfer?"
- Verify experimentally the properties of rotations, reflections, and translations.
- Lines are taken to lines, and line segments to line segments of the same length.
- Angles are taken to angles of the same measure.
- Parallel lines are taken to parallel lines.
- Understand that a two-dimensional figure is congruent to another if the second can be obtained from the first by a sequence of rotations, reflections, and translations; given two congruent figures, describe a sequence that exhibits the congruence between them.
- Describe the effect of dilations, translations, rotations, and reflections on two-dimensional figures using coordinates.
- Understand that a two-dimensional figure is similar to another if the second can be obtained from the first by a sequence of rotations, reflections, translations, and dilations; given two similar two-dimensional figures, describe a sequence that exhibits the similarity between them.
- Use informal arguments to establish facts about the angle sum and exterior angle of triangles, about the angles created when parallel lines are cut by a transversal, and the angle-angle criterion for similarity of triangles.
Dilations/Rigid Transformations
KEY IDEAS
Alternate Interior AnglesInterior angles are angles that are made by a transversal crossing two parallel lines. They are the angles that lie between the parallel lines, not outside them.If two interior angles lie on opposite sides of the transversal they are called alternate interior angles.In the figure, a and b are alternate interior angles, and b and c are also alternate interior angles.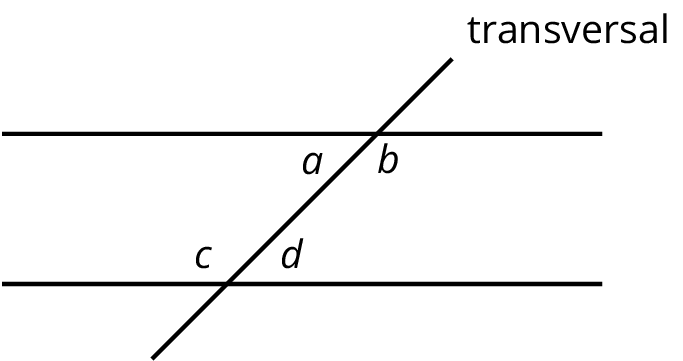
ClockwiseAn object is rotating clockwise if it is turning in the same way that the hour or minute hand goes around a clock.The tilted square is rotated 15∘ clockwise from the square sitting horizontally on its base.
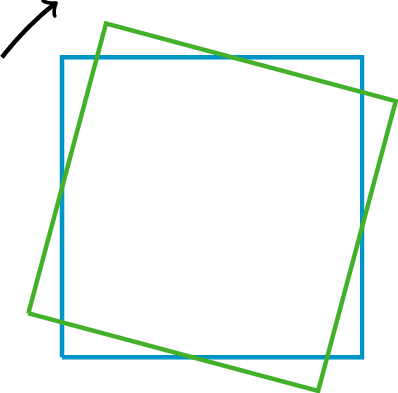CongruentOne figure is congruent to another if there is a rigid transformation (a sequence of translations, rotations, and reflections) that moves the first figure so that it fits exactly over the second. The second figure is called the image of the rigid transformation.Triangle A is congruent to triangle D. A translation takes triangle A to triangle B, a rotation takes triangle B to triangle C, and a reflection takes triangle C to triangle D.
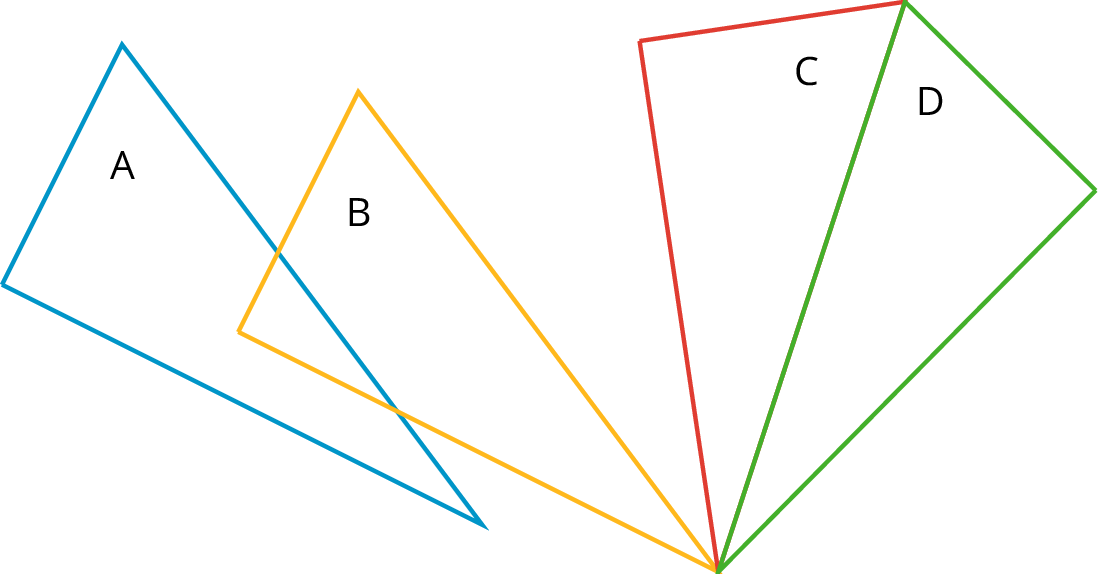CorrespondingIf a part of the original figure matches up with a part of the copy, we call them corresponding parts. The part could be an angle, point, or side, and you can have corresponding angles, corresponding points, or corresponding sides.If you have a distance between two points in the original figure, then the distance between the corresponding points in the copy is called the corresponding distance.CounterclockwiseAn object is rotating counterclockwise if it is turning in the opposite way to the way that the hour or minute hand goes around a clock.The tilted square is rotated 15∘ counterclockwise from the square with a horizontal base.
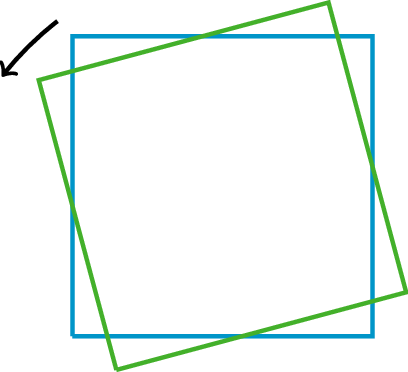ImageTranslations, rotations, and reflections move objects in the plane. Points, segments, and other parts of the original all have corresponding parts on the “moved object.” The moved object is called the image.For example, here is triangle ABC and a translation to the right and up which is labeled DEF.Point F in the image corresponds to point C, segment EF in the image corresponds to segment BE, and angle DEF corresponds to angle ABC.
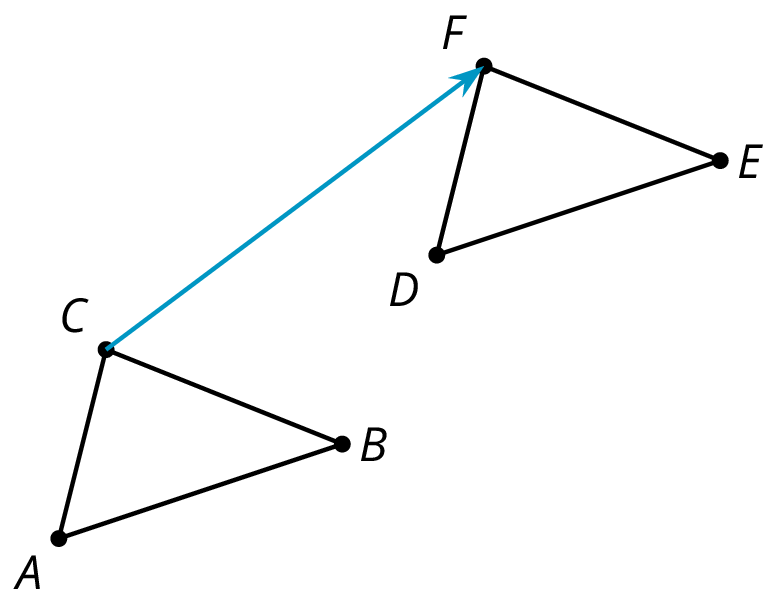Rigid transformationA rigid transformation is a sequence of translations, rotations, and reflections. If a rigid transformation is applied to a geometric figure, the resulting figure is called the image of the original figure under the transformation. The diagram shows a rigid transformation consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the image of the first triangle under this rigid transformation.
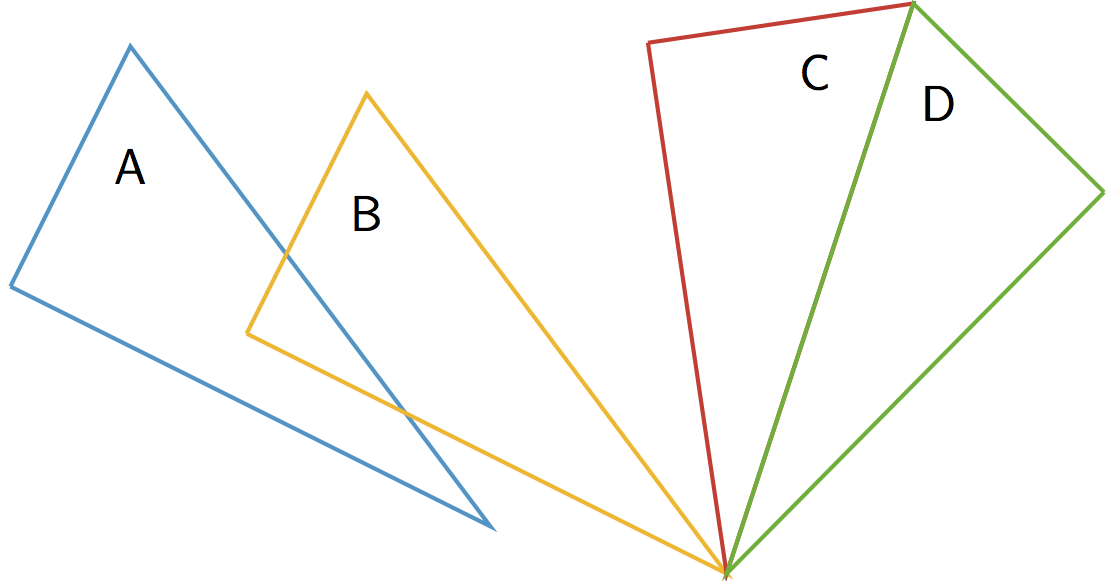ReflectionThe reflection of a figure across a line takes every point of the figure to a point directly opposite to it on the other side of the line and the same distance from the line. In the figure, the triangle B is the reflection of the triangle A across the line ℓ .
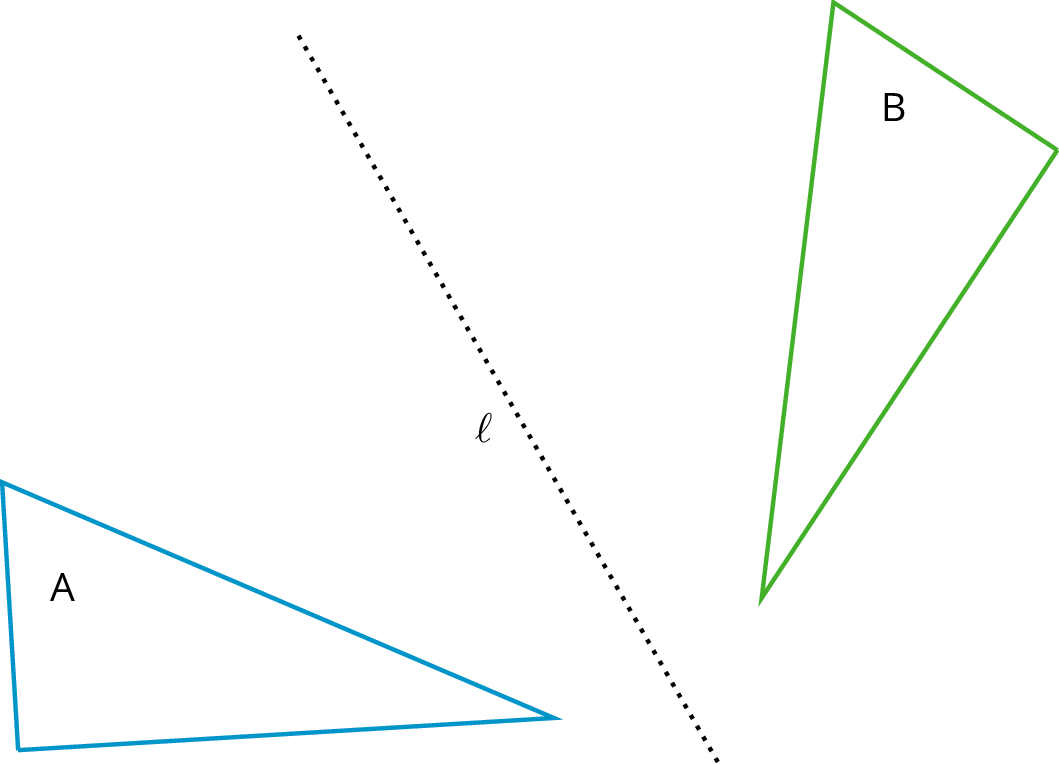RotationA rotation has a center, an angle, and a direction. It moves every point of a figure in a circle around the center, in the direction specified (clockwise or counterclockwise), and for a distance specified by the angle. For example, in the figure, triangle A is rotated 55∘ clockwise about center O to get triangle B .
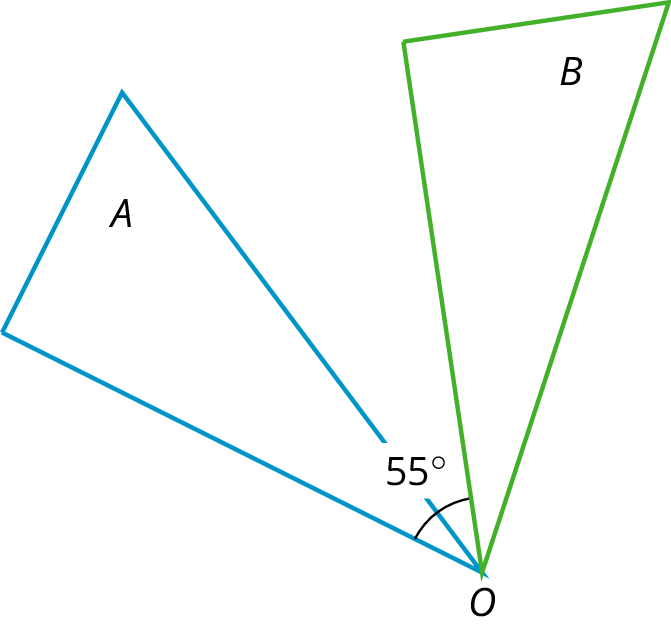Sequence of TransformationsA sequence of transformations is a set of translations, rotations, reflections, and dilations performed in a particular order on a geometric figure, resulting in a final figure. The diagram shows a sequence of transformations consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the final figure resulting from the sequence.Straight Angle If the two rays that make an angle form a straight line, we call the angle a straight angle.TransformationA transformation is a translation, rotation, reflection, or dilation, or combination of these. There is also a more general concept of a transformation of the plane that is not discussed in grade 8.TranslationA translation has a distance and a direction. It moves every point in a figure the given distance in the given direction.The figure on the left is translated to the figure on the right in the direction from A to B , using the distance from A to B .
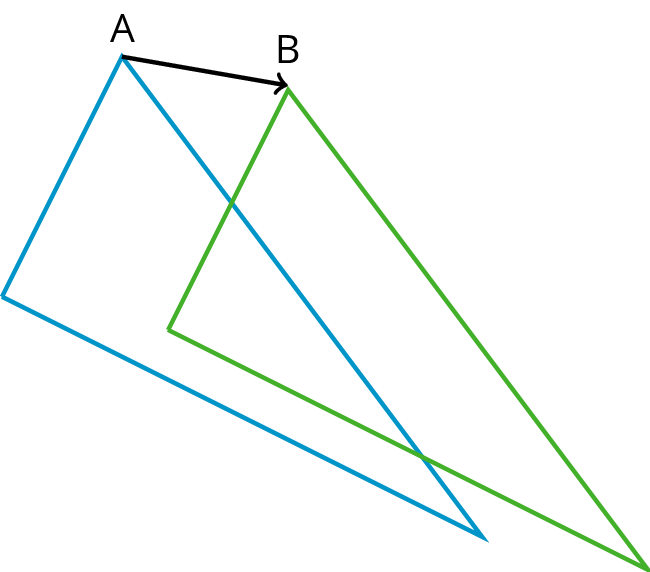Transversal A transversal to two parallel lines is a line that cuts across them, intersecting each one.Vertical AnglesA pair of vertical angles is a pair of angles that are across from each other at the point where two lines intersect. There are two pairs of vertical angles.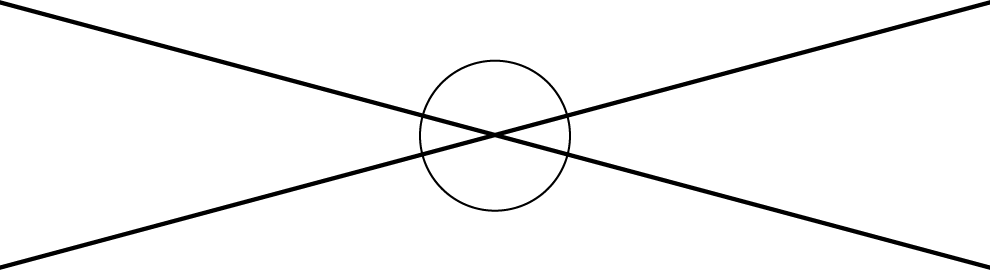
ClockwiseAn object is rotating clockwise if it is turning in the same way that the hour or minute hand goes around a clock.The tilted square is rotated 15∘ clockwise from the square sitting horizontally on its base.CongruentOne figure is congruent to another if there is a rigid transformation (a sequence of translations, rotations, and reflections) that moves the first figure so that it fits exactly over the second. The second figure is called the image of the rigid transformation.Triangle A is congruent to triangle D. A translation takes triangle A to triangle B, a rotation takes triangle B to triangle C, and a reflection takes triangle C to triangle D.CorrespondingIf a part of the original figure matches up with a part of the copy, we call them corresponding parts. The part could be an angle, point, or side, and you can have corresponding angles, corresponding points, or corresponding sides.If you have a distance between two points in the original figure, then the distance between the corresponding points in the copy is called the corresponding distance.CounterclockwiseAn object is rotating counterclockwise if it is turning in the opposite way to the way that the hour or minute hand goes around a clock.The tilted square is rotated 15∘ counterclockwise from the square with a horizontal base.ImageTranslations, rotations, and reflections move objects in the plane. Points, segments, and other parts of the original all have corresponding parts on the “moved object.” The moved object is called the image.For example, here is triangle ABC and a translation to the right and up which is labeled DEF.Point F in the image corresponds to point C, segment EF in the image corresponds to segment BE, and angle DEF corresponds to angle ABC.Rigid transformationA rigid transformation is a sequence of translations, rotations, and reflections. If a rigid transformation is applied to a geometric figure, the resulting figure is called the image of the original figure under the transformation. The diagram shows a rigid transformation consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the image of the first triangle under this rigid transformation.ReflectionThe reflection of a figure across a line takes every point of the figure to a point directly opposite to it on the other side of the line and the same distance from the line. In the figure, the triangle B is the reflection of the triangle A across the line ℓ .RotationA rotation has a center, an angle, and a direction. It moves every point of a figure in a circle around the center, in the direction specified (clockwise or counterclockwise), and for a distance specified by the angle. For example, in the figure, triangle A is rotated 55∘ clockwise about center O to get triangle B .Sequence of TransformationsA sequence of transformations is a set of translations, rotations, reflections, and dilations performed in a particular order on a geometric figure, resulting in a final figure. The diagram shows a sequence of transformations consisting of a translation (from A to B) followed by a rotation (from B to C) followed by a reflection (from C to D). The last triangle is the final figure resulting from the sequence.Straight Angle If the two rays that make an angle form a straight line, we call the angle a straight angle.TransformationA transformation is a translation, rotation, reflection, or dilation, or combination of these. There is also a more general concept of a transformation of the plane that is not discussed in grade 8.TranslationA translation has a distance and a direction. It moves every point in a figure the given distance in the given direction.The figure on the left is translated to the figure on the right in the direction from A to B , using the distance from A to B .Transversal A transversal to two parallel lines is a line that cuts across them, intersecting each one.Vertical AnglesA pair of vertical angles is a pair of angles that are across from each other at the point where two lines intersect. There are two pairs of vertical angles.