Vielecke
Vielecke (Polygone) sind geometrische Figuren. Das kleinste Vieleck ist das Dreieck, das größte hat unendlich viele Ecken (ist aber kein Kreis!)
Die folgenden Polygone sind für dich wichtig:
1. Dreieck
2. Viereck
3. Fünfeck
4. Sechseck
5. Achteck
6. Regelmäßiges Vieleck (n-Eck)
Die Winkelsumme im n-Eck beträgt:
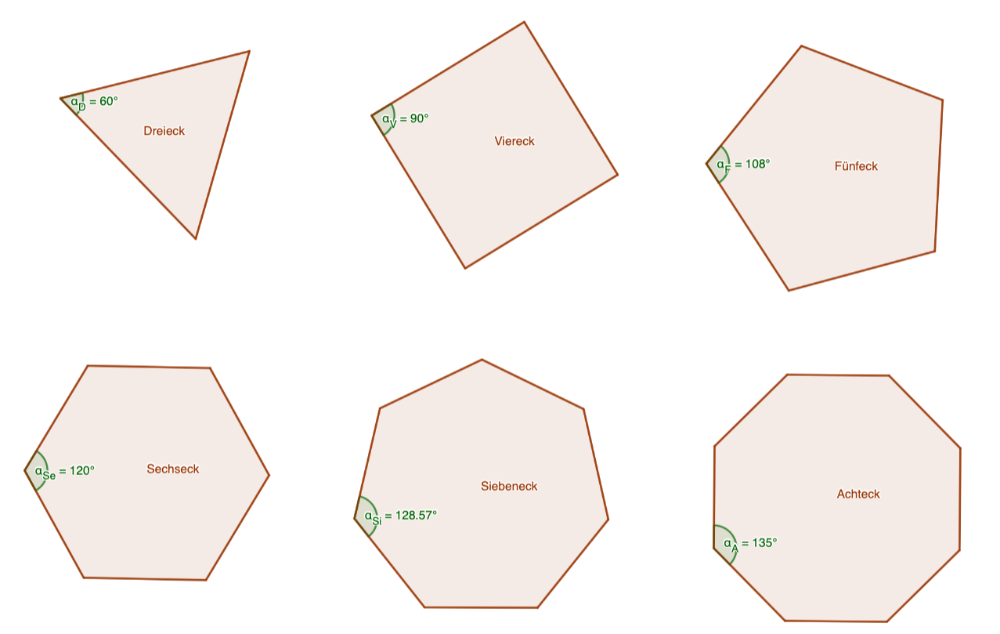
Hier siehst du eine Übersicht von regelmäßigen Vielecken mit dem passenden Innenwinkel.
Fünfeck
![[math]A=\frac{5\cdot a\cdot h_a}{2}[/math][size=85]
[math]A=\frac{5\cdot r^2}{2}\cdot sin72°[/math]
[math]u=5a[/math]
[/size]](https://www.geogebra.org/resource/rfvkee4v/kAzYTQxpmuoYfhed/material-rfvkee4v.png)
Sechseck
Beim regelmäßigen Sechseck gilt: r = a
![[size=85][math]A=\frac{3\cdot a^2}{2}\cdot\sqrt{3}[/math]
[math]u=6a[/math][/size]](https://www.geogebra.org/resource/vtxkqqyx/VGCgwUeyDxQhDdfr/material-vtxkqqyx.png)
Achteck
Hier siehst du das regelmäßige Achteck
![[size=85][math]A=\frac{8\cdot a\cdot h_a}{2}[/math]
[math]A=\frac{8\cdot r^2}{2}\cdot sin45°[/math]
[math]u=8a[/math]
[/size]](https://www.geogebra.org/resource/mrydd9nb/SqJZfhB9bTgzbDiZ/material-mrydd9nb.png)
Regelmäßiges Vieleck (n-Eck)
Es gelten folgende Formeln: (n steht für die Anzahl der Ecken)