Pointwise Convergence
Pointwise Convergence Explained
This concept is often contrasted with uniform convergence. To say that
means that
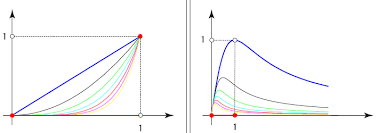
That is a stronger statement than the assertion of pointwise convergence: every uniformly convergent sequence is pointwise convergent, to the same limiting function, but some pointwise convergent sequences are not uniformly convergent. For example, if 
is a sequence of functions defined by 
, then 
pointwise on the interval [0,1), but not uniformly.The pointwise limit of a sequence of continuous functions may be a discontinuous function, but only if the convergence is not uniform. For example,
takes the value 1 when x is an integer and 0 when x is not an integer, and so is discontinuous at every integer.The values of the functions fn need not be real numbers, but may be in any topological space, in order that the concept of pointwise convergence make sense. Uniform convergence, on the other hand, does not make sense for functions taking values in topological spaces generally, but makes sense for functions taking values in metric spaces, and, more generally, in uniform spaces.
means that
That is a stronger statement than the assertion of pointwise convergence: every uniformly convergent sequence is pointwise convergent, to the same limiting function, but some pointwise convergent sequences are not uniformly convergent. For example, if is a sequence of functions defined by , then pointwise on the interval [0,1), but not uniformly.The pointwise limit of a sequence of continuous functions may be a discontinuous function, but only if the convergence is not uniform. For example,
takes the value 1 when x is an integer and 0 when x is not an integer, and so is discontinuous at every integer.The values of the functions fn need not be real numbers, but may be in any topological space, in order that the concept of pointwise convergence make sense. Uniform convergence, on the other hand, does not make sense for functions taking values in topological spaces generally, but makes sense for functions taking values in metric spaces, and, more generally, in uniform spaces.