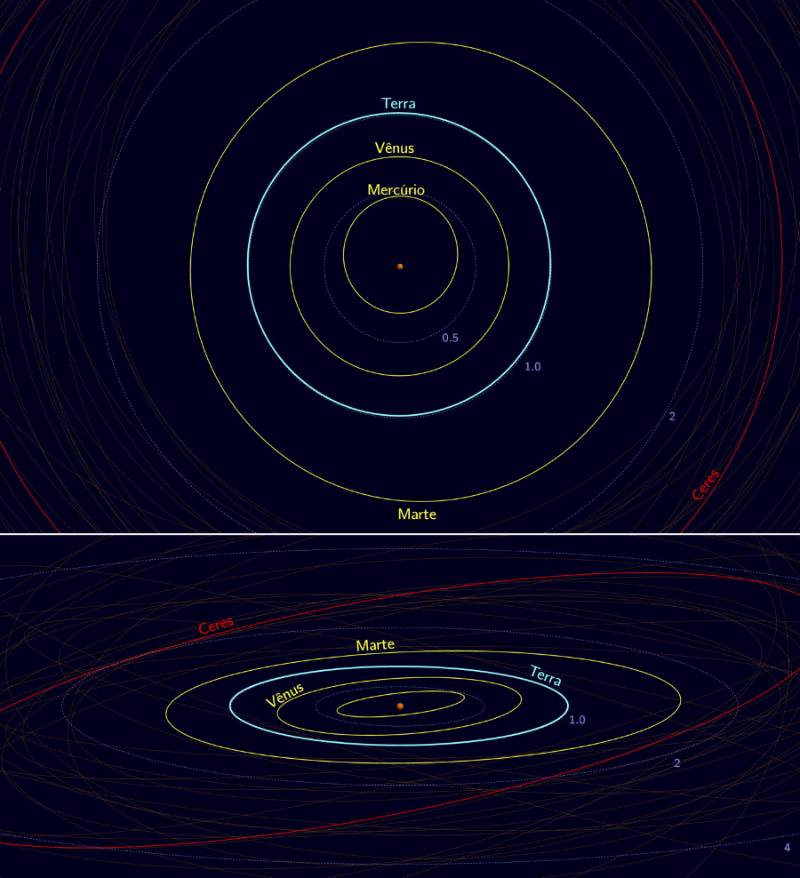
Elipse
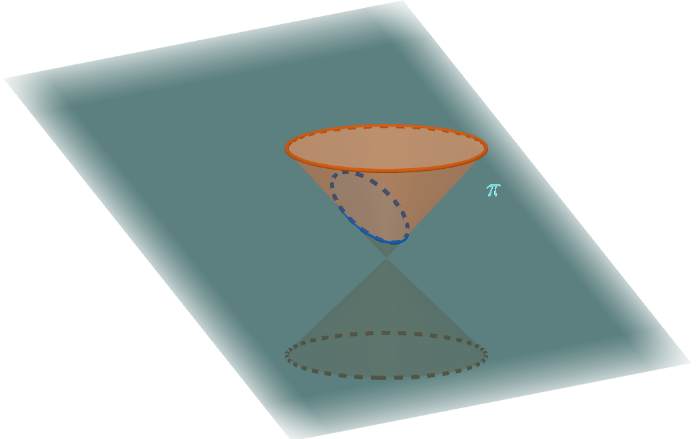
Em termos matemáticos, a elipse é um lugar geométrico definida pelos pontos no plano cartesiano cuja a distância a dois pontos fixos é constante, isto é, Caso não saiba o que é lugar geométrico, clique no link (https://impa.br/wp-content/uploads/2020/01/PAPMEM_JAN_2020_LG1-Papmem.pdf). Vamos nomear esses dois pontos fixos de e . Note que eles podem ser pontos quaisquer do plano. Estes pontos são chamados de focos. Nesta primeira interação com o Geogebra, siga alguns passos e observe o que está acontecendo. 1) Mova o ponto "P(x,y)" e observe os valores no canto superior esquerdo. 2) Altere a posição dos pontos "F1" e "F2" para gerar outra elipse e, em seguida realize novamente o passo 1.
Equação da elipse
Demonstração da elipse
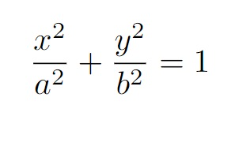
Agora responda as perguntas a seguir
O que acontece quando altero os valores de a?
O que acontece quando altero os valores de b?
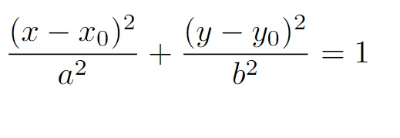
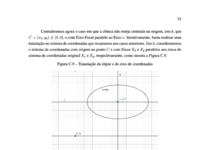
Demonstração elipse transladada
Agora responda as perguntas a seguir
O que acontece quando altera o valor de ?
O que acontece quando altera o valor de ?