Raízes da Função:
As raízes de uma função quadrática: são os valores de "x" nos quais a função assume o valor zero. Em outras palavras, são os pontos no gráfico da função onde a parábola cruza o eixo x. Para determinar as raízes de uma função quadrática, você pode seguir estas etapas:
Considere a função quadrática na forma geral:
f(x) = ax^2 + bx + c
- Defina a função igual a zero: ax^2 + bx + c = 0
- Use a fórmula quadrática para encontrar as raízes:
A fórmula quadrática é dada por:
x = (-b ± √(b^2 - 4ac)) / (2a)
- Calcule o discriminante (a parte dentro da raiz quadrada) usando os coeficientes "a," "b" e "c": Discriminante = b^2 - 4ac
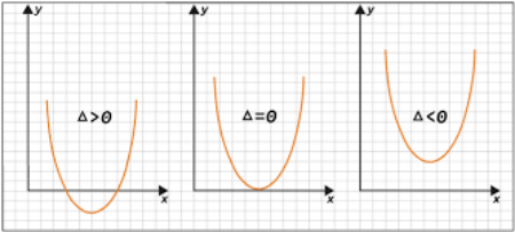
- Agora, você pode usar a fórmula quadrática para calcular as raízes. Lembre-se de que pode haver duas raízes reais (quando o discriminante é positivo), uma raiz real (quando o discriminante é igual a zero) ou nenhuma raiz real (quando o discriminante é negativo).
- As raízes são representadas por "x1" e "x2," e elas podem ser encontradas substituindo os valores do discriminante na fórmula quadrática: x1 = (-b + √(b^2 - 4ac)) / (2a) x2 = (-b - √(b^2 - 4ac)) / (2a)