Divisão Regular do Plano

Para construir suas figuras complexamente simétricas, Escher utilizou a simples ideia de que alguns polígonos que são capazes de pavimentar todo um plano. Entre os polígonos utilizados por Escher podemos destacar triângulos equiláteros, paralelogramos, deltoides e hexágonos regulares. Seu conjunto de obras construídas através da pavimentação de polígonos é conhecido como Divisão Regular do Plano.
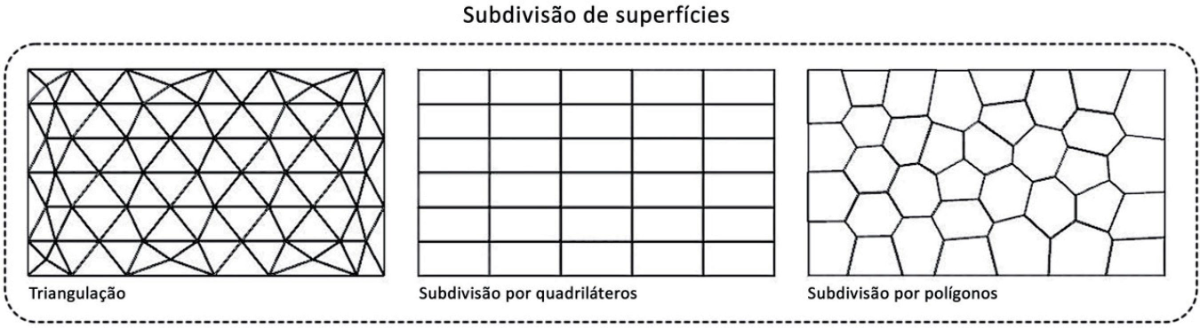
Tipos de Subdivisões
Existem diversos métodos de subdivisões de planos e superfícies. A figura acima ilustra três dos métodos mais utilizados: a triangulação, a subdivisão por quadriláteros e a subdivisão por polígonos de cinco ou mais lados. Estes três métodos serão destacados neste trabalho, sobretudo porque embasam os principais trabalhos e técnicas desenvolvidas por M. C. Escher. No entanto, é importante mencionar que não são apenas polígonos que conseguem subdividir o plano, podemos subdividir o plano utilizando formas curvilíneas.
Para mais detalhes, acesse o artigo abaixo:
https://www.scielo.br/pdf/inter/v18n3/1518-7012-inter-18-03-0003.pdf
Pavimentações Arquimedianas
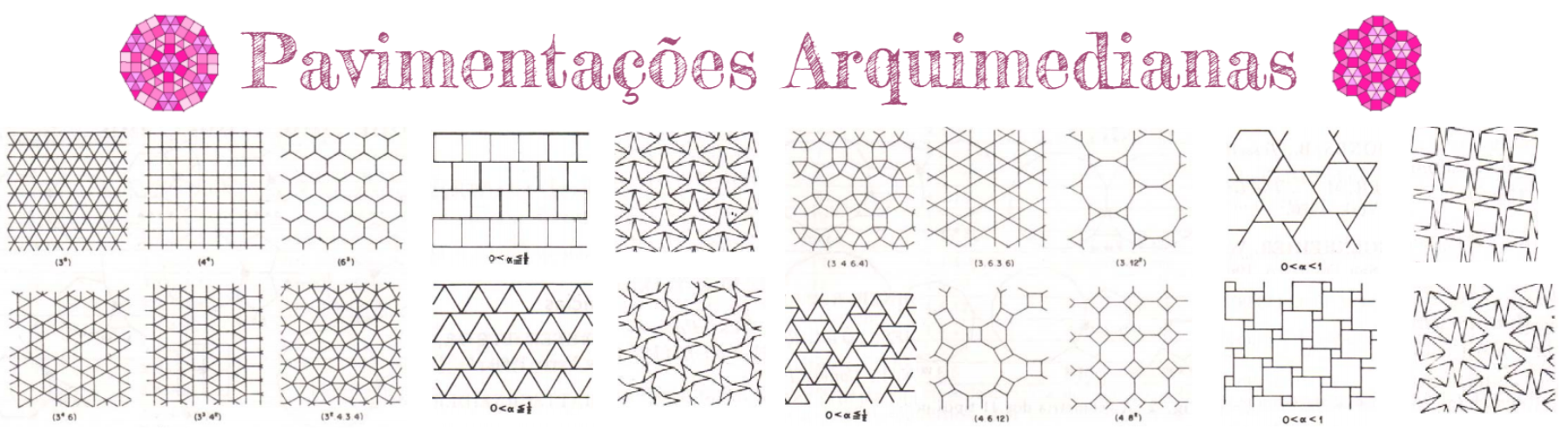
Pavimentações Arquimedianas
Entre os diferentes tipos de pavimentações poligonais podemos destacar as pavimentações arquimedianas. Estas são pavimentações formadas por dois ou mais polígonos regulares e em que os vértices da pavimentação são todos do mesmo tipo.
Não é necessário que um polígono seja regular para ser capaz pavimentar o plano, contudo, as Pavimentações Arquimedianas são muito exploradas principalmente por apresentarem um grau complexo de restrições que limitam o número de possibilidades.
Para mais detalhes, acesse o artigo abaixo:
http://www.periodicos.rc.biblioteca.unesp.br/index.php/bolema/article/view/10673/7057