15. Parábola: Construção
Objetivo: Fixado o foco e diretriz construir a parábola
Um pouco de teoria. Lembres que fixado um ponto (foco) e uma reta (diretriz) define-se a parábola determinada por esses elementos como sendo o conjunto
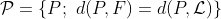 Isto é, o conjunto de ponto no plano (determinado pelo foco e diretriz) cuja distância até o foco e diretriz é a mesma. Neste applet obteremos este conjunto (parábola) utilizando um pouco de geometria.
Passo1: Aqui você determina a diretriz e a posição do foco que desejar. A diretriz é determinada pela equação
Isto é, o conjunto de ponto no plano (determinado pelo foco e diretriz) cuja distância até o foco e diretriz é a mesma. Neste applet obteremos este conjunto (parábola) utilizando um pouco de geometria.
Passo1: Aqui você determina a diretriz e a posição do foco que desejar. A diretriz é determinada pela equação
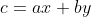
No canto superior direito poderá inserir os valores dos parâmetros desejados.
Passo2: Aqui escolhemos um ponto na diretriz (isto permitirá obter o segmento ). O objetivo desse ponto é poder construir a parábola utilizando argumento de geometria elementar.
Passo3: Obtido o segmento do passo 2 construimos duas retas: A mediatriz do segmento e a reta perpendicular à diretriz no ponto . Lembremos que a mediatriz de um dado segmento é a reta perpendicular ao segmento traçada no seu ponto médio. Estas duas retas sempre se interceptam (para isso bastará garantir que o foco não esteja na diretriz). O ponto de interseção é denotado por
Passo4: Como o ponto pertence à mediatriz do segmento então o triângulo é isósceles com base . Assim . Por outro lado, tendo em vista que o ponto também pertence à reta ortogonal a (diretriz) posando por . Conclusão, o ponto obtido é um elemento da parábola (de foco e diretriz ). Movimentando o ponto se obterá todos os outros da parábola procurada.
Passo5: Clique neste passo para mostrar a parábola o foco e diretriz.
No canto superior direito poderá inserir os valores dos parâmetros desejados.
Passo2: Aqui escolhemos um ponto na diretriz (isto permitirá obter o segmento ). O objetivo desse ponto é poder construir a parábola utilizando argumento de geometria elementar.
Passo3: Obtido o segmento do passo 2 construimos duas retas: A mediatriz do segmento e a reta perpendicular à diretriz no ponto . Lembremos que a mediatriz de um dado segmento é a reta perpendicular ao segmento traçada no seu ponto médio. Estas duas retas sempre se interceptam (para isso bastará garantir que o foco não esteja na diretriz). O ponto de interseção é denotado por
Passo4: Como o ponto pertence à mediatriz do segmento então o triângulo é isósceles com base . Assim . Por outro lado, tendo em vista que o ponto também pertence à reta ortogonal a (diretriz) posando por . Conclusão, o ponto obtido é um elemento da parábola (de foco e diretriz ). Movimentando o ponto se obterá todos os outros da parábola procurada.
Passo5: Clique neste passo para mostrar a parábola o foco e diretriz.