Многоугольники
Многоугольники
Рассмотрим фигуру, составленную из отрезков так, что смежные отрезки (т. е. отрезки AB и BC, BC и CD,..., FA и AB не лежат на одной прямой, а несмежные отрезки не имеют общих точек. Такая фигура называется многоугольником. Точки A, B, C, ... , F называются вершинами, а отрезки AB, BC, CD, ..., EF, FA сторонами многоугольника. Сумма длин всех сторон называется периметром многоугольника.
Многоугольник
Многоугольник с n вершинами называется n-угольником; он имеет n сторон. Примером многоугольника является треугольник. На рисунке изображены четырехугольник ABCD и шестиугольник A1,A2,A3,A4,A5,A6.
Четырёхугольник и шестиугольник
Две вершины многоугольника, принадлежащие одной стороне, называются соседними. Отрезок, соединяющий любые две несоседние вершины, называется диагональю многоугольника.
Соседние стороны и диагонали многоугольника
Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая - внешней областью многоугольника.
Внутренняя и внешняя части многоугольника
Задания
На рисунке изображен многоугольник
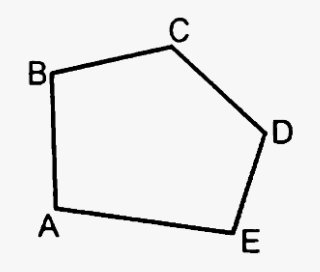
Укажите количество сторон и диагоналей в данном многоугольнике