hiperbola
Foku izeneko F1 eta F2 puntuak eta hiperbolaren konstantea izeneko k distantzia emanda [k<dist(F1,F2)], F1-erako eta F2-rako distantzien arteko kendura berdin k-ren balio absolutua duten P puntuen leku geometrikoari hiperbola esaten diogu:
dist(P,F1) - dist(P,F2)=k
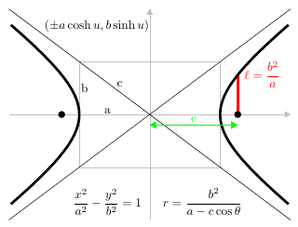
k=2a
c>a
Hiperbolaren zentroa O(o1,o2) bada:
Eszentrikotasuna: hiperbola baten eszentrikotasuna beti e>1
e=c/a
Hiperbola bertikalean edo horizontalean egon ahal da.
- Horizontalean: x-ren zatikia positiboa da. Zentroa O(o1,o2) bada:
- Fokuak kalkulatzeko:
- Erpinak kalkulatzeko:
- Asintotak kalkulatzeko:
Kalkulatu hurrengo irudiaren hiperbolaren datuak (a,b eta c ,eta fokuak, eta A erpinak , eszentrikotasuna eta asintotak). Gero idatzi hiperbolaren ekuazioa beste eratan.
2. Bertikalean: y-ren zatikia positiboa da. Zentroa O(o1,o2) bada:
- Fokuak kalkulatzeko:
- Erpinak kalkulatzeko:
- Asintotak:
Kalkulatu hurrengo irudiaren hiperbolaren datuak (a,b eta c ,eta fokuak, eta A erpinak , eszentrikotasuna eta asintotak). Gero idatzi hiperbolaren ekuazioa beste eratan.