Parábola
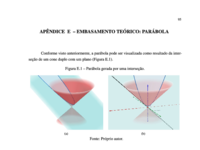
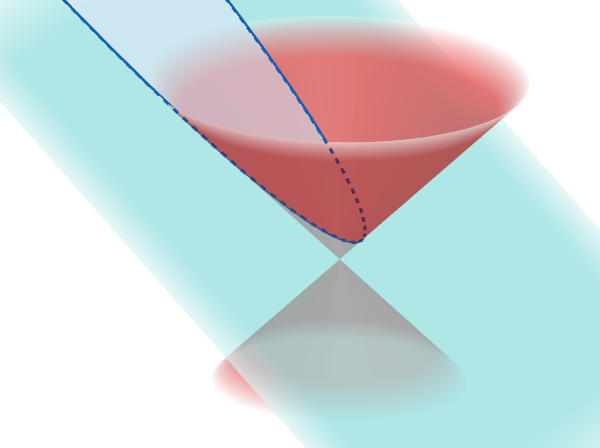
Construindo a parábola do mesmo modo que Apolônio, através da intersecção de um plano com um cone duplo, teremos o seguinte lugar geométrico.
A parábola é um conteúdo que os estudante costumam a ver no nono ano do ensino fundamental e retomado como função quadrática no primeiro ano do ensino médio. Existem muitas aplicações no cotiado que passam despercebidas pela população? Um exemplo é comunicação através dos satélites, onde o usuário instala uma antena parabólica em sua residência e começa a receber o sinal. Este tipo de antena é mais comum para assinantes de televisões fechadas. O nome antena parabólica vem do conteúdo que iniciaremos a seguir.
Matematicamente falando foi estudado o conteúdo de parábola juntamente com a equação do segundo grau, ou seja, e para encontrar a raiz deste polinômio utiliza-se a conhecida fórmula de Bhaskara (). No primeiro ano do ensino médio dar-se-á continuidade no conteúdo como uma função, por exemplo, , chamada que função quadrática.
Na janela a seguir podemos relembrar visualmente o que acontece quando variamos os coeficientes da função.
Definimos parábola como sendo um conjunto de todos os pontos que estão a mesma distância da reta e do foco , ou seja, .
O foco já conhecemos das outras cônicas. A reta é chamada de reta diretriz e a reta perpendicular a que passa pelo ponto é chamada de eixo focal. Na janela a seguir temos o foco, o ponto e no canto superior direito as distâncias. Siga as orientações para verificar.
1) Mova o ponto e verifique o que está acontecendo com as distâncias.
2) Mova o foco e repita o passo anterior.
Note que os valores das distâncias são iguais, ou seja, até mesmo quando altera-se o foco.
Equação da parábola
Acabamos de construir a parábola através da definição. Sabemos muitas equações que geram gráficos do mesmo formato, entretanto conhecemos a equação onde o foco não é abordado, portanto precisamos investigar para descobrir uma equação que permita encontrar o foco da parábola de modo simples.
A partir da definição chega-se a equação reduzida da parábola de modo sutil. Note que na definição aparece um elemento que não tínhamos trabalhado anteriormente com as demais cônicas, a posição de reta diretriz . Esta fará uma grande diferença na posição da parábola.
No primeiro caso trabalharemos com a reta diretriz paralela ao eixo e o foco e acima dela.
Para facilitar os cálculos trabalharemos com o vértice da parábola centrada na origem. Novamente temos dois caminhos que fica a cargo do leitor escolher, diretamente a equação reduzida ou deduzi-la através da definição. Caso queria conhecer a demonstração matemática clique no arquivo a seguir, caso contrário continuemos.
Demonstração da parábola
Os valores de e (distância do foco ao vértice) são reais, portanto é comum aparecer radicais e fração que serão eliminados nas operações.
Equação reduzida da parábola é:
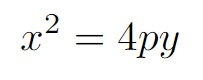
Na janela a seguir insira a equação e perceba que automaticamente aparecerá um controle deslizante para a variável . Mude o valor de através do controle para verificar o que acontece com a parábola.
Note que a parábola possui seu vértice sobre a origem e de acordo com o valor de , a parábola muda a concavidade. Se realizarmos um pensamento análogo a descentralização da elipse, chegaremos a equação a seguir:
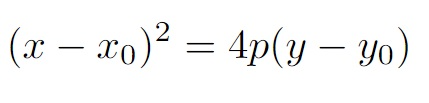
Caso queira entender como encontrar esta equação clique no arquivo.
Demonstração parábola transladada
Nesta segunda etapa vamos investigar o que acontece se trocarmos por na equação anterior, ou seja,.
Note que se desenvolvermos a equação, supondo valores para , e , obtemos:
Veja que a incógnita está elevada ao quadrado e não o .
Agora vamos construir na janela a seguir a parábola nos seguintes passos.
1° Digite no canto superior esquerdo, ao lado do + a equação .
2° Utilize os controles deslizantes para observar o que está acontecendo com a parábola para diferentes valores de .
Observe que a parábola apresenta a concavidade para direita ou esquerda dependendo do valor de . Esclarecendo o que foi visto no primeiro ano do ensino médio, onde as parábolas construídas apresentavam apenas a concavidade para cima ou para baixo, isso acontece pois era trabalhado em função de , agora estamos estudando geometria analítica e não funções.
Na próxima janela de interação vamos investigar o que acontece se mudarmos o termo quadrático.
1° Digite no canto superior esquerdo, ao lado do + a equação .
2° Utilize os controles deslizantes para observar o que está acontecendo com a parábola para diferentes valores de .
É muito importante conhecer estes conceitos para facilitar a construção do projeto do telescópio.
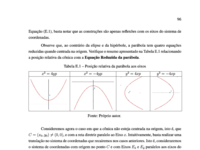
Resumindo
Anote o quadro a seguir em seu caderno.
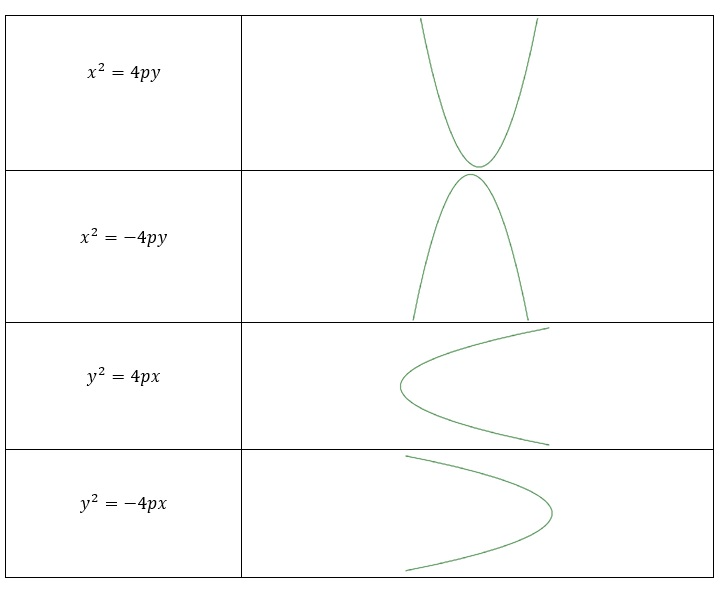
Exercício
Siga os passos a seguir para encontrar a equação reduzida da parábola.
Na janela a seguir construa uma parábola em que seu foco seja um ponto aleatório e a reta diretriz também. Encontre a equação reduzida.
1° Coloque um ponto qualquer no plano cartesiano, desde que o ponto não pertença a reta.
2° Vá ao ícone 
e utilize a ferramenta 
para construir a parábola.
3° Na equação da parábola no canto esquerdo clique nos três pontinhos e clique em "Configurações".
4° No canto direito abriu uma aba, clique em "Álgebra".
5° Escolha a equação "".
Note que no canto esquerdo está a equação procurada.
e utilize a ferramenta para construir a parábola.
3° Na equação da parábola no canto esquerdo clique nos três pontinhos e clique em "Configurações".
4° No canto direito abriu uma aba, clique em "Álgebra".
5° Escolha a equação "".
Note que no canto esquerdo está a equação procurada.