Perpendicular Bisectors in Right Triangles (have to do construction)
Investigate properties of the perpendicular bisectors of the 'legs' in a right triangle by following the instructions below the image.
#1 - Create perpendicular bisectors for each of the 'legs' of the right triangle. Click the icon and then the menu item shown below (do this in the applet at the top of the site). Then click on each of the legs to create the perpendicular bisectors to those sides.
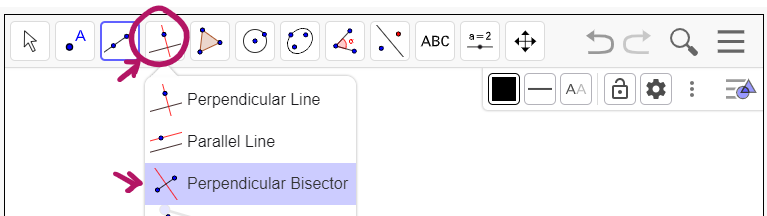
What do you notice about where the perpendicular bisectors intersect? Do you think this is true for all right triangles?
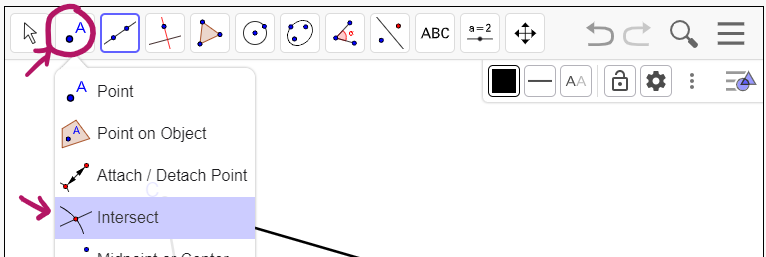
#2 - Put a point where the two perpendicular bisectors intersect. Click the icon and the menu item shown below. Then click on each of the perpendicular bisectors you created in the step above. This will put point D on the point where the intersect.
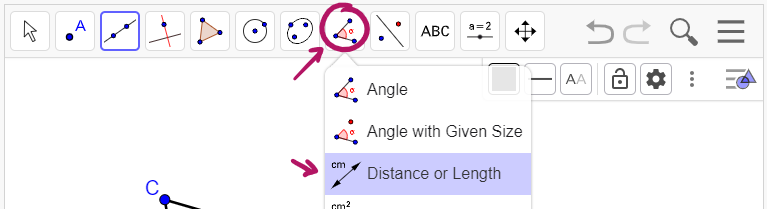
#3 - Measure the distance from the point, D, where the perpendicular bisectors intersect to the endpoints of the hypotenuse. Click the icon and then the menu item shown below. Click on point A then point D - the measured distance between them will appear. Then click on point B and D - the measured distance between them will appear.
Observations:
1. You will need to click the arrow in the top left of the applet
2. Drag the points on the triangle around to change the shape.
3. What do you notice about the distance from where the perpendicular bisectors intersect (point D) and the endpoints of the hypotenuse? What property does this show always exists in right triangles?