x-t图像
一、图像是什么?
直线运动中,每个时刻物体在坐标系中都有对应的一个位置,这个位置可以用一个正数或负数坐标来表示。
我们将这个位置坐标和对应的时间一一记录下来,就成了物体的位置时间图像。
只有直线运动的位置坐标用一个数字就可以表示,例如表示物体在坐标系中这个位置上。
二维以上的运动确定位置需要更多的坐标,因此图像只能描述直线运动。
二、x-t图像如何读?
在图像中,我们关心的信息有物体运动的位置、位移、和速度。
1、读取位置
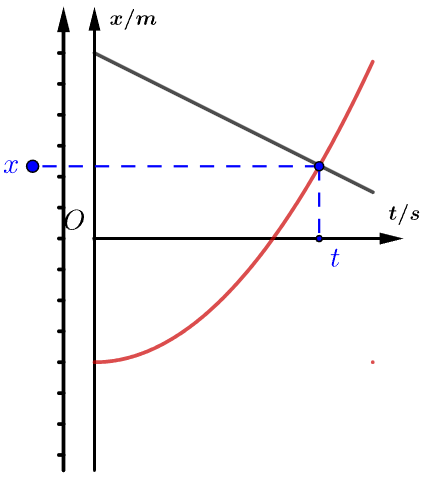
图像中,纵轴就是物体运动的坐标系,直接读出点的纵坐标就是位置。
将图像的位置坐标投射到纵轴上,根据每个时刻的物体位置,我们可以直接读出物体运动的情况。
在同一个x-t图像中,两条线的交点意味着两个运动物体同一时刻处于同一位置,我们把这种现象叫相遇。

2、读取位移
位移,在图像中,只需要找到和时刻对应的位置坐标和,两者相减即可。
读位移时注意,和分别对应初末时刻和,要找准时间和位置上的先后顺序,然后确定位移方向。
位移大小在图像上是两点纵坐标之间的线段长。
3、读取平均速度
我们先补充一下数学中斜率的概念。
三个斜面,同样往前走20m,分别上升10m、15m、20m,哪个更陡呢?
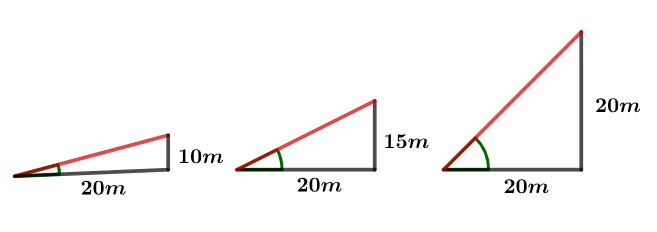 明显上升20m的斜面更陡。
为了衡量平面直角系里一条直线的倾斜程度,我们可以借鉴这种比较方法。
用上升的高度比上水平所走,看往前移动单位长度,相应会上升多少高度。
这个比值叫做斜率,常用字母表示,越大,就说明直线越倾斜。
明显上升20m的斜面更陡。
为了衡量平面直角系里一条直线的倾斜程度,我们可以借鉴这种比较方法。
用上升的高度比上水平所走,看往前移动单位长度,相应会上升多少高度。
这个比值叫做斜率,常用字母表示,越大,就说明直线越倾斜。
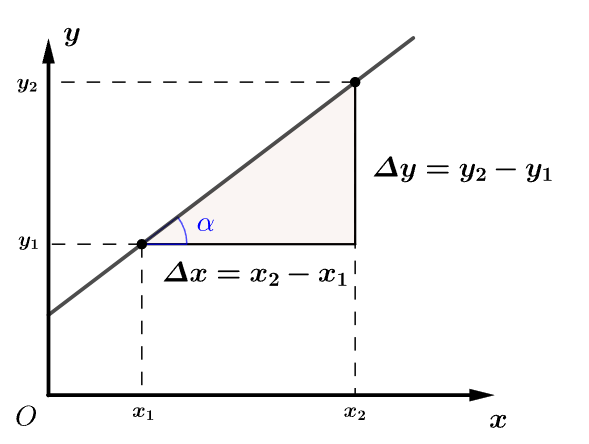 倾斜直线与水平方向的夹角叫做倾斜角,例如上图中的。倾斜角越大,直线越倾斜。
倾斜角和斜率都可以表示直线的倾斜程度。
从图中我们可以看出,我们前面所求的比值实际上正是倾斜角的正切值。
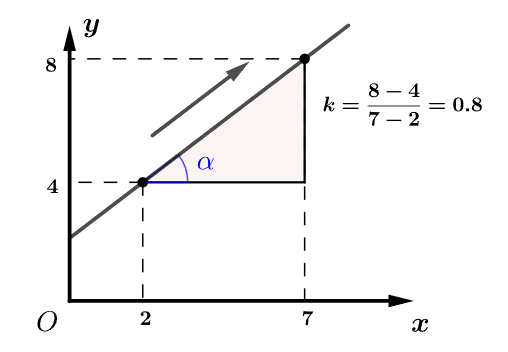
在平面直角坐标系中,只要知道直线上任意两点(,)和()就可以求出其斜率。
,其中,。
斜率有正负之分,就像山有上坡和下坡之分。沿x轴正方向,向上走为正,向下走为负。
计算时要注意,不能直接用长度去比,还要看倾斜方向添加正负号。
倾斜直线与水平方向的夹角叫做倾斜角,例如上图中的。倾斜角越大,直线越倾斜。
倾斜角和斜率都可以表示直线的倾斜程度。
从图中我们可以看出,我们前面所求的比值实际上正是倾斜角的正切值。
在平面直角坐标系中,只要知道直线上任意两点(,)和()就可以求出其斜率。
,其中,。
斜率有正负之分,就像山有上坡和下坡之分。沿x轴正方向,向上走为正,向下走为负。
计算时要注意,不能直接用长度去比,还要看倾斜方向添加正负号。
 斜率为正
斜率为正
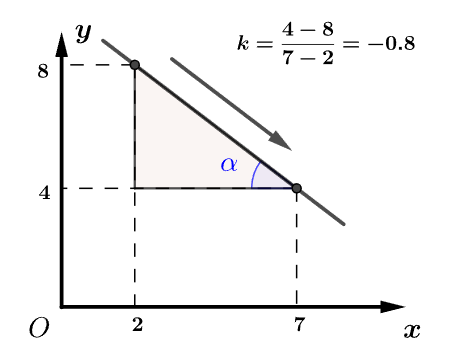 斜率为负
对于曲线,我们将曲线上不同两点之间连线叫作割线。割线斜率的求法和直线一样。
斜率为负
对于曲线,我们将曲线上不同两点之间连线叫作割线。割线斜率的求法和直线一样。
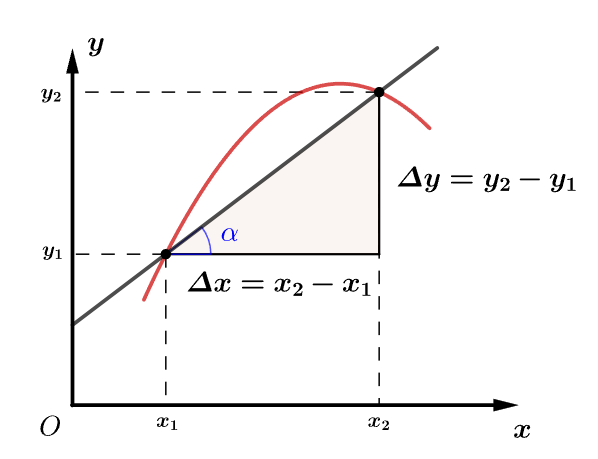 然后我们再来看,图像中平均速度如何读取:
然后我们再来看,图像中平均速度如何读取:
 明显上升20m的斜面更陡。
为了衡量平面直角系里一条直线的倾斜程度,我们可以借鉴这种比较方法。
用上升的高度比上水平所走,看往前移动单位长度,相应会上升多少高度。
这个比值叫做斜率,常用字母表示,越大,就说明直线越倾斜。
明显上升20m的斜面更陡。
为了衡量平面直角系里一条直线的倾斜程度,我们可以借鉴这种比较方法。
用上升的高度比上水平所走,看往前移动单位长度,相应会上升多少高度。
这个比值叫做斜率,常用字母表示,越大,就说明直线越倾斜。
 倾斜直线与水平方向的夹角叫做倾斜角,例如上图中的。倾斜角越大,直线越倾斜。
倾斜角和斜率都可以表示直线的倾斜程度。
从图中我们可以看出,我们前面所求的比值实际上正是倾斜角的正切值。
在平面直角坐标系中,只要知道直线上任意两点(,)和()就可以求出其斜率。
,其中,。
斜率有正负之分,就像山有上坡和下坡之分。沿x轴正方向,向上走为正,向下走为负。
计算时要注意,不能直接用长度去比,还要看倾斜方向添加正负号。
倾斜直线与水平方向的夹角叫做倾斜角,例如上图中的。倾斜角越大,直线越倾斜。
倾斜角和斜率都可以表示直线的倾斜程度。
从图中我们可以看出,我们前面所求的比值实际上正是倾斜角的正切值。
在平面直角坐标系中,只要知道直线上任意两点(,)和()就可以求出其斜率。
,其中,。
斜率有正负之分,就像山有上坡和下坡之分。沿x轴正方向,向上走为正,向下走为负。
计算时要注意,不能直接用长度去比,还要看倾斜方向添加正负号。
 斜率为正
斜率为正
 斜率为负
对于曲线,我们将曲线上不同两点之间连线叫作割线。割线斜率的求法和直线一样。
斜率为负
对于曲线,我们将曲线上不同两点之间连线叫作割线。割线斜率的求法和直线一样。
 然后我们再来看,图像中平均速度如何读取:
然后我们再来看,图像中平均速度如何读取:在图像中,无论是不是匀速直线运动,时间的平均速度都是、时刻对应两点连线的斜率。
斜率的值越大,表示物体的运动速度越快。
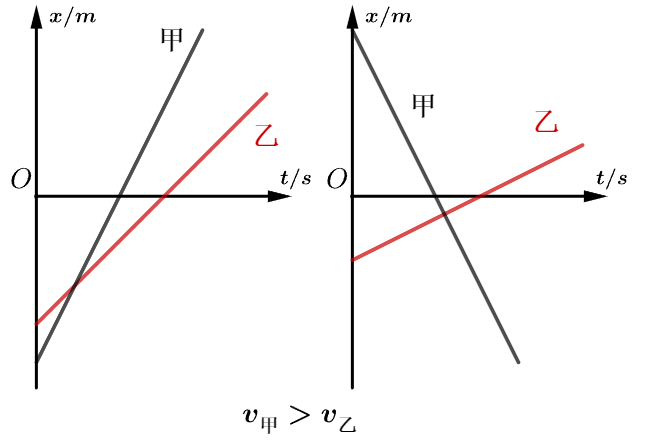 斜率为正表示速度方向为正,物体沿坐标系正方向运动:
斜率为正表示速度方向为正,物体沿坐标系正方向运动:
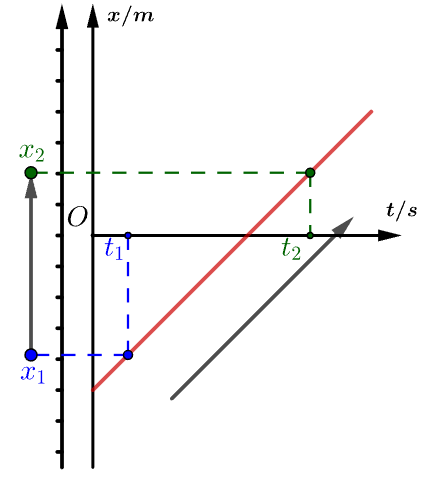 斜率为负表示物体速度方向为负,物体沿坐标系负方向运动:
斜率为负表示物体速度方向为负,物体沿坐标系负方向运动:
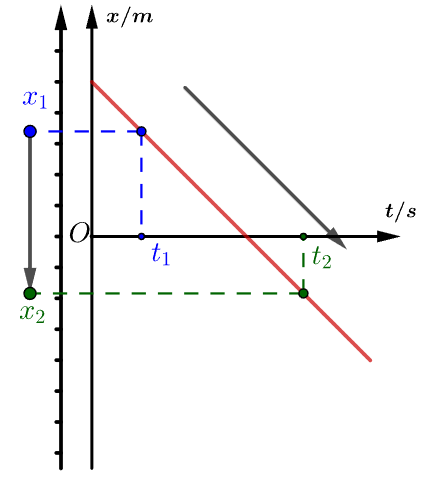
 斜率为正表示速度方向为正,物体沿坐标系正方向运动:
斜率为正表示速度方向为正,物体沿坐标系正方向运动:
 斜率为负表示物体速度方向为负,物体沿坐标系负方向运动:
斜率为负表示物体速度方向为负,物体沿坐标系负方向运动:

4、读取瞬时速度
匀速直线运动每个时刻的瞬时速度都等于平均速度,图像中可以用直线的斜率直接去表示。
非匀速直线运动则需要另辟蹊径。
实际应用中切线的斜率可以借助切点和切线与坐标轴的交点来求取。
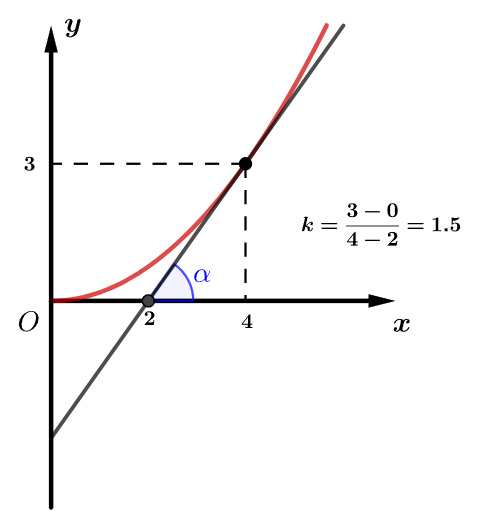 除此之外,在数学里有专门求切线斜率的工具——导数,有兴趣的同学可以自己去了解。
多数时候我们不用求出切线的斜率,只需要比较切线的斜率大小,从而判断一个物体的速度变化即可。
除此之外,在数学里有专门求切线斜率的工具——导数,有兴趣的同学可以自己去了解。
多数时候我们不用求出切线的斜率,只需要比较切线的斜率大小,从而判断一个物体的速度变化即可。
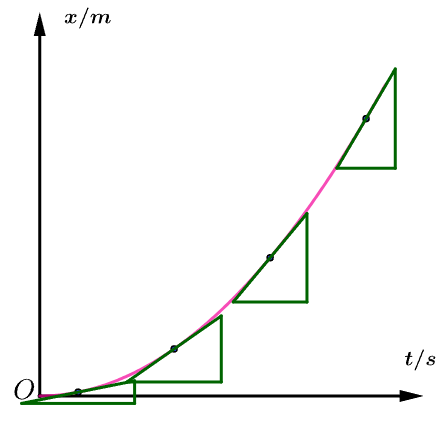
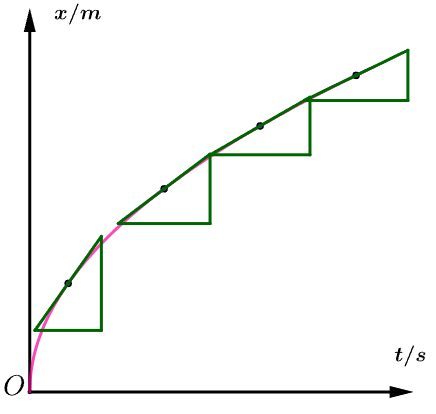
 斜率变大,速度逐渐变大
斜率变大,速度逐渐变大
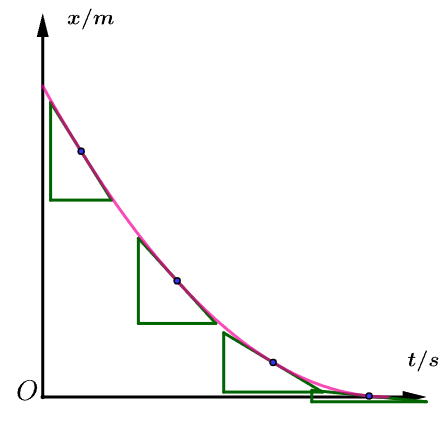
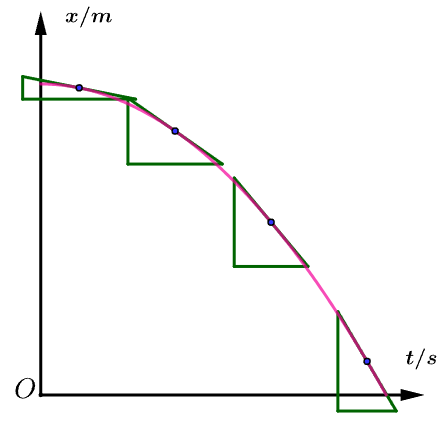
 斜率变小,速度逐渐变小
斜率变小,速度逐渐变小
 除此之外,在数学里有专门求切线斜率的工具——导数,有兴趣的同学可以自己去了解。
多数时候我们不用求出切线的斜率,只需要比较切线的斜率大小,从而判断一个物体的速度变化即可。
除此之外,在数学里有专门求切线斜率的工具——导数,有兴趣的同学可以自己去了解。
多数时候我们不用求出切线的斜率,只需要比较切线的斜率大小,从而判断一个物体的速度变化即可。

 斜率变大,速度逐渐变大
斜率变大,速度逐渐变大

 斜率变小,速度逐渐变小
斜率变小,速度逐渐变小