Unmögliche Perspektive
Das Gegenstück zur unmöglichen Figur ist die unmögliche Perspektive: ein ebenes Bild, das nicht durch eine Projektion aus einem realen oder virtuellen 3D Objekt entstanden ist, sondern eine Art freier Skizze ist, eine Collage, die Elemente mehrerer Projektionen vereint.
Das ist in der Kunst durchaus ein gebräuchliches Stilmittel.
Aber ist es vielleicht doch überraschend, so etwas auch in Mathematik-Schulbüchern zu finden (Dank an Hans Walser für den Hinweis).
Immer wieder findet man dort Darstellungen von Würfel mit Kugel, in denen der Würfel in schräger und die Kugel in senkrechter Parallelperspektive dargestellt ist. Entstanden sind solche Bilder dann wohl in dem Bemühen der Grafiker, die 'schönen' Teile zweier Perspektiven in einem Bild zu vereinen, was ich Grafiker-Perspektive nennen möchte.
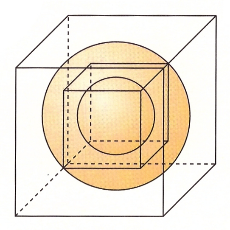
Dass diese Grafiker-Perspektive zu einem Artefakt, neudeutsch zu einem Fake führt, sehen eher nur geschulte Mathematiker. Denn bei einer schrägen Parallelprojektion (z. B. Kavalierprojektion) müsste das Bild der Kugel eine Ellipse sein, bei einer senkrechten Parallelprojektion (z. B. Dimetrie) müssten die rechten Winkel bei den Würfelkanten verzerrt sein.
Allgemein wird das Bild aber nicht als 'falsch' erkannt. Im Vergleich zu den 'wahren' Bildern bei schräger oder senkrechter Parallelprojektion werden viele Betrachter sogar der Meinung sein, dass diese Grafiker-Perspektive 'schöner aussieht'.
Damit wird bewusst oder unbewusst eine Maxime der Kubisten des vorigen Jahrhunderts umgesetzt:
"Immer muß das Objekt unter dem aufschlußreichsten Winkel gezeigt werden ... Es wird manchmal sogar mehrere Blickpunkte enthalten können; es wird sich manchmal so zeigen, wie es uns niemals zu sehen möglich ist." (J. Rivière 1912, zitiert nach Jooss 2000).