Teorema de Pappus-Guldin


Primer Teorema
El área, A de una superficie de revolución generada mediante la rotación de una curva plana C alrededor de un eje externo a C sobre el mismo plano, es igual a la longitud de C, s, multiplicada por la distancia, d, recorrida por su centroide en una rotación completa alrededor de dicho eje.
Centroide:
-Centro de masa de un objeto con densidad uniforme.
-Para un objeto unidimensional uniforme de longitud L, el centroide es el punto medio del segmento de línea.
-Para un triángulo, el centroide es el punto de intersección de sus tres medianas.
-El centroide de una figura geométrica es el centro de simetría. Para cualquier otro objeto de forma irregular de dos dimensiones, el centroide es el punto donde un soporte simple puede equilibrar este objeto. Por lo general, el centroide de un objeto bidimensional o tridimensional se encuentra utilizando integrales dobles o triples.
Ejemplos
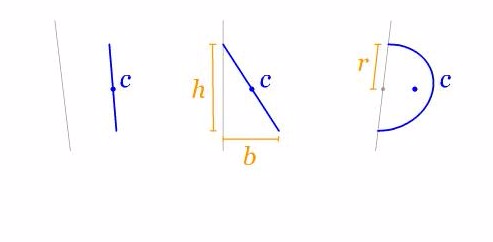
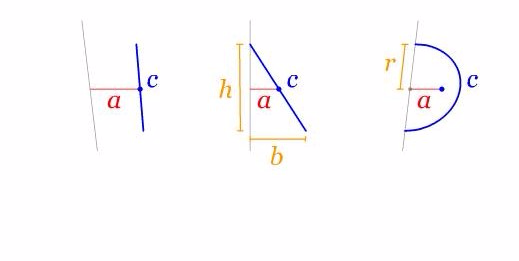
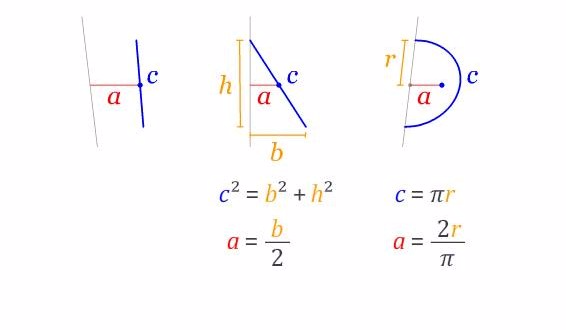
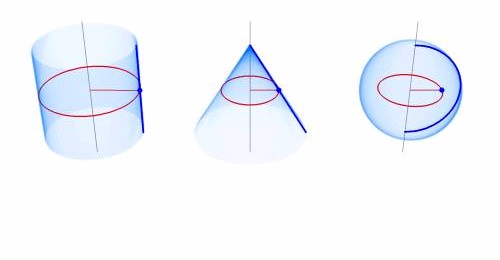
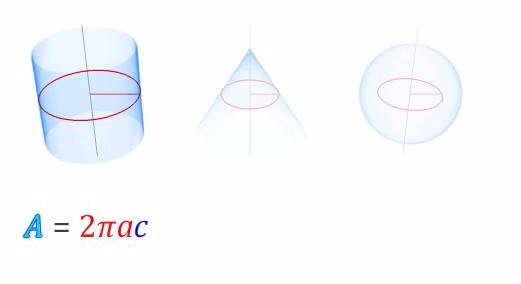
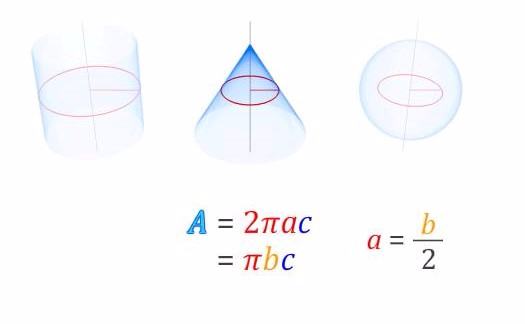
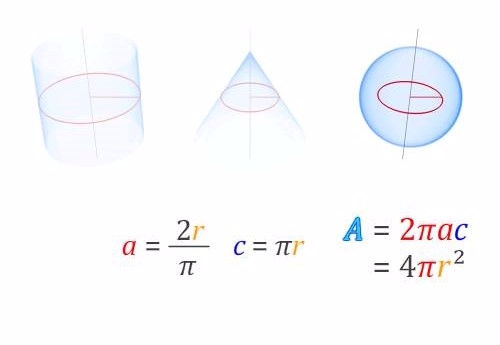
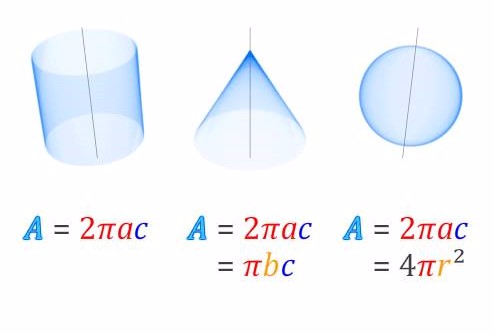
Demostración del centroide de una semicircunferencia
Teorema 2
El volumen, V, de un sólido de revolución generado mediante la rotación de un área plana alrededor de un eje externo, es igual al producto del área, A, por la distancia, d recorrida por su centroide en una rotación completa alrededor del eje.
V=Ad
Aplica tus aprendizajes
Resuelve los siguientes ejercicios