Eliminating Time
The kinematic equations discussed until this point all contain the time variable. This is for obvious reasons since how things move through space depends on the passage of time. Nonetheless, we can do some mathematics to eliminate time from the equations. This is worth doing, provided that it serves a good purpose.
The purpose that it serves is that we can determine a relationship between speed and distance that can be useful in certain cases. For instance, if we know that a ball is dropped from a 4.0m high balcony, we can find the speed at which it strikes the ground without having to first determine the duration of time for which it fell. Or consider shooting an object upward and wondering how high it will go based on the launch speed. If you don't care to know the time of flight and just want to know how high it gets, then this section will be a more efficient way to obtain such answers.
The methods of this section also serves us well when the acceleration of an object depends on position or on velocity as well - and those can be very interesting cases to learn about. They apply to situations with springs, ones with air drag, and others.
The Mathematics of Eliminating the Time Variable
The relationship that we are after is one that relates velocity to position, and yet contains no explicit time variable. In a mathematical sense, what we seek to find is how velocity changes in relation to a change in position, or but that immediately looks troublesome! The big problem is that a derivative is related to division (before the limit is taken in the definition of the derivative), and division by a vector is an undefined operation. So what we must do is deal individually with components of those vectors, since the components themselves are scalar quantities. Therefore, our second attempt is going to be to find the quantity where is understood to be shorthand for The trick to arrive at the right expression is to use the chain rule of differentiation.
Here is the clever trick we need to get a useful expression: If we use the chain rule for the derivative of velocity (acceleration), we get:
Doing this allows us to rewrite the expression in terms of familiar quantities. Here is how it continues:
It is at this point that we will pause for a moment to consider how to proceed. There are multiple ways to continue depending on the details of the problem. Really it's all about the acceleration term.
Any of these three situations can be dealt with:
- A constant-valued acceleration
- An acceleration that depends on position (as is true of springs and molecular bonds, etc.)
- An acceleration that depends on velocity such as viscous drag or quadratic air drag.
Constant Acceleration Solution
Given a constant acceleration we shuffle terms, and then integrate both sides. The integrals are trivial to evaluate, as you see below:
Given this result, we can find the speed at a position given another speed at a different position provided we know the value of constant acceleration Notice that we technically do not know the direction of travel since the velocity's component is squared! As inconvenient as this is, it does tell us something about the nature of such problems. Since time is absent, the equations don't really know future from past!
While you may be thinking the terms with the subscript zeros come first in time and the other terms come later, the equations don't know that. It is for this reason that you always get two answers for - one that is true if time runs the way you think it does, and the other result for time running into the past. Just ignore the answer you aren't looking for.
To clarify, while we may wish to use this equation to answer a simple question about how fast a rock should be falling after having been dropped and having fallen 30cm from our hand, the equations will tell you that there are two possibilities. The first one is the answer you're looking for. The other one will tell you that a rock rising at the same speed (opposite sign on v) from a position 30cm below your hand will eventually end up at rest in your hand. This is just the reverse (in time) of the previous scenario.
So really the math is sensible, it's just that the equations don't know which way time is running- into the future or into the past.
Acceleration that Depends on Position
An example of a position-dependent acceleration is a mass attached to a spring. The farther the spring gets stretched in one direction, for instance, the faster the mass will accelerate in the other direction.
Another very similar example is a skater on a half-pipe. If the half-pipe is assumed to be parabolic in shape (they aren't quite in reality), then the slope grows linearly with displacement from the center of the pipe. This must be the case since the derivative of a quadratic is linear.
For relatively small angles below around 30 degrees, the acceleration on an incline is proportional to the slope of the incline. Double the slope and acceleration is doubled. In the next chapter we'll see what happens to the acceleration regardless of whether the slope is small or not.
In any case, for both the spring and the half-pipe we would find that the acceleration in the x-direction is given by a function that looks like this: The constant c, in the case of the half-pipe, would grow larger with the concavity of the half-pipe. For the spring, c grows larger for a stiffer spring and also for a smaller mass. Those details are for discussions later in the book.
A Half-Pipe with Curve Fit
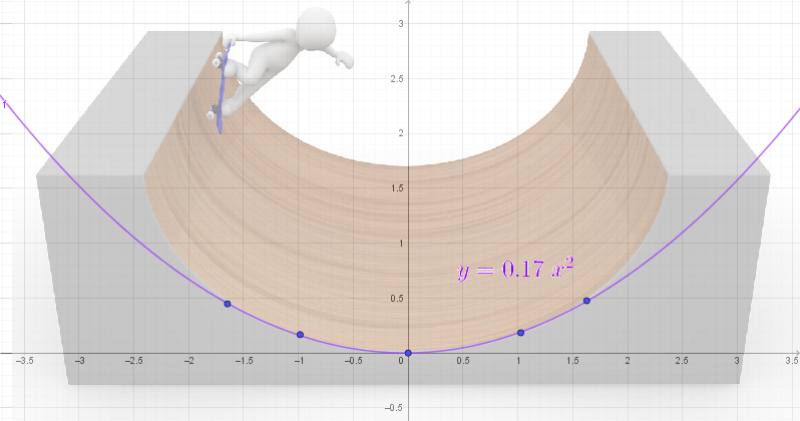
Let's consider the half-pipe in the illustration above. The slope of the pipe is the derivative, so we'd get The inverse meters are added so that we have the correct units. The units must be inverse meters since x will be in meters and slope is unitless.
As mentioned above, the acceleration is proportional to the slope for small angles. The expression for the acceleration is where 'g' is earth's gravitational field strength. This means that for the half-pipe in the picture, the acceleration would be
So now let's suppose the skater starts from rest at a position 1.5m to the left of the bottom of the pipe. How fast will they be rolling when they reach the bottom of the half-pipe? Here's how the math works:
Notice that the negative solution means that if a skater starts at the bottom going LEFTWARD at 2.77m/s, that they will eventually end up coming to rest 1.5m to the left of the starting position. That's the whole issue of having two roots and no sense of forward or backward progression in time.
Acceleration Depending on Velocity in 1D
We discussed earlier in the book that there are two types of resistance that objects experience when moving through fluids. Viscous drag depends linearly on velocity and air drag and others depend quadratically on velocity.
Besides fluid resistance, it happens to be the case that rolling resistance for vehicles with wheels (trains, cars, bikes) can be modeled quite well by a function that depends on velocity to the first power (linearly), just like viscous drag. At slow speeds - maybe under 5-10mph for a bike and under 40mph or so for a car - the major resistive force is rolling resistance, whereas at higher speeds it is air drag that dominates.
Suppose we want to predict how far a car will roll given an initial starting speed of 10m/s. The reason it will slow down and stop is that there is rolling resistance associated with the fact that the part of the tire that contacts the road (the contact patch) deforms (flattens) as the tire rolls. This means a force resists its rolling motion. From another angle, it means energy is lost in deforming the contact patch. The loss of energy results in the car slowing down and eventually coming to rest. But energy is a later discussion in the text.
Since rolling resistance (force and resulting acceleration) is proportional to velocity, suppose we did some measurements of a particular car and found that when coasting on level ground Once again the units of the constant are chosen so that units on both sides of the equation match. That acceleration would mean, for instance, that if the car is traveling at 10m/s in the +x direction, that rolling resistance will cause the acceleration to be -2m/s in the -x direction. As the car slows, so will the rate at which it loses speed be less, or the magnitude of the acceleration will be smaller.
If that car starts out rolling at 10m/s on level ground, let's see if we can find out how far it should coast before coming to rest. In this case, you’ll see that acceleration is a function of
Another way to look at this result is to plot the x-component of velocity as a function of distance. If we do this, we get So the y-intercept is the initial x-component of velocity and the function decreases linearly until the car stops. To continue to follow the function until the velocity's component goes negative is really not meaningful. It would somehow imply that rolling resistance would eventually reverse the vehicle and send it back the way it came - which it does not.
Looking at the result, obviously the faster the car starts out, the farther it rolls. What's interesting is that the relationship is so simple. It is linear. That means starting at twice the speed, it'll roll twice as far. Triple the initial speed and it goes three times as far, etc. Of course this is only true if we neglect other forces like air drag which become more important as speed rises. We'll deal with those details later in the course.
Another thing to mention is this: With constant resistive forces (which leads to constant acceleration), an object will NOT slide or roll twice as far with twice the initial speed. From earlier discussions in this section, you should be able to work out how much farther it will travel before coming to rest. See if you can do that.