Parametrizando
Una de las cualidades de la Geometría Dinámica que la ha hecho particularmente beneficiosa para el aprendizaje de la matemática, es la capacidad de actualizar una construcción a medida que se varía un objeto matemático (un punto, una recta, un número).
Uno de los recursos didácticos tradicionales en la ejercitación que se propone a los alumnos, ha sido analizar la variación de cierta expresión algebraica en función de un parámetro variable. Por ejemplo, analizar las características de una recta de ecuación y = mx al variar m. Este tipo de construcciones se realizan muy sencillamente en Geogebra, añadiendo deslizadores como el que ejemplificamos a continuación, donde podemos mover el punto negro variando el valor de m (en este caso, entre -10 y 10):
Ejemplo de construcción
En la ventana de GeoGebra que aparece debajo:
Introducir en la zona de entrada:
- a=1
- b=1
- y=a x+b (Nótese que hay un espacio entre la a y la x)
Deslizadores
Una alternativa es crear los deslizadores directamente, con la herramienta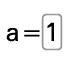 
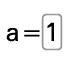. En el cuadro de diálogo emergente se podrá elegir el nombre, los extremos del intervalo de variación, el incremento, y decidir si tratará de un deslizador numérico o angular, entre otros.
En adelante bastará usar el nombre asignado al deslizador para operar con él.
. En el cuadro de diálogo emergente se podrá elegir el nombre, los extremos del intervalo de variación, el incremento, y decidir si tratará de un deslizador numérico o angular, entre otros.
En adelante bastará usar el nombre asignado al deslizador para operar con él.Ejercicio
Realiza una construcción con dos deslizadores: a, variando entre 0 y 3; y b, variando entre -5 y 5. Luego representar la función dada por f(x)=a x+b.
¿Qué preguntas propondrías a tus alumnos para analizar el comportamiento de este gráfico al mover los deslizadores?